Creating Custom Unit Averagers

This tutorial shows how to create custom unit averagers for cases where built-in methods (like OptimalUnitAverager) don’t fit your needs. By subclassing BaseUnitAverager and implementing _compute_weights(), you can design weighting schemes tailored to your data. As an example, this tutorial implements an exponential weighted averager.

By the end, you should be able to:

1. Understand the anatomy of an averager class.

2. Implement a custom averager.

Functionality covered

BaseUnitAverager: implementing _compute_weights().

import pandas as pd
from docs_utils import plot_germany, prepare_frankfurt_example
from numpy import exp
from numpy.linalg import norm

from unit_averaging import BaseUnitAverager

Following along

If you would like to follow along on a local machine, please download the contents of the data folder here . To recreate the plots, also download the docs_utils.py file .

Introduction

Different weighting schemes in the weighted averages of unit averaging serve different purposes. For example:

• The optimal averaging scheme of OptimalUnitAverager (see the Getting Started page) is tailored towards estimating unit-level parameters with minimum mean squared error.

• The equal weights scheme of MeanGroupUnitAverager yields an excellent estimator of the average target parameter.

One can also conveniently create custom averaging schemes that target different parameters of interest or use different fitting logic. Such custom averagers may use domain-specific information, incorporate external data, or use further distributional information of the heterogeneous units.

A Look at BaseUnitAverager

To understand how to define custom averagers, it is useful to take a brief look at the BaseUnitAverager class. BaseUnitAverager itself is an abstract base class, and all the in-built and custom unit averagers should derive from it.

BaseUnitAverager implements several keys pieces of logic:

• The fit() and average() methods (see Getting Started).

• Input processing: under the hood, all inputs related to individual units are converted to NumPy arrays.

• Handling the target ID (target_id argument of fit()): the index of the target unit in the processed individual estimates array is stored in the _target_coord attribute.

To create a custom averager, you need to implement _compute_weights(), which defines how weights are assigned to each unit. If you need arguments besides the focus function and the individual estimates, you also need to redefine the constructor.

Defining an Exponentially Weighted Averager

To illustrate how to build a custom averager, we now implement an exponentially weighted averager. This scheme assigns weights based on the distance between each unit’s estimated coefficients and the target unit’s coefficients.

Weight Scheme

Formally, let \(\hat{\theta}_i\) be the estimated coefficient vector for unit \(i\) (an element of ind_estimates). We define the weight \(w_i\) of unit \(i\) in the averaging estimator as

\[w_i = \dfrac{\exp(-||\hat{\theta}_i - \hat{\theta}_{target}||)}{ \sum_{j=1}^N \exp(-||\hat{\theta}_j - \hat{\theta}_{target}||) },\]

where \(||\cdot||\) is the Euclidean norm. This scheme gives more weights to units whose coefficient estimates are more similar to the target unit.

In contrast to the optimal weight scheme of OptimalUnitAverager, this weight scheme does not take variance information into account, making it potentially less efficient.

Defining the Averager

We can now create our ExpDistUnitAverager by inheriting from BaseUnitAverager and implementing the exponential weights.

Observe that the weights \(w_i\) can be computed just from the target ID and the collection of individual estimates. In such cases, one does not have to redefine or expand the constructor obtained from BaseUnitAverager. We only need to implement the _compute_weights() method that assigns the weights attribute as a result:

class ExpDistUnitAverager(BaseUnitAverager):
    def _compute_weights(self):
        """Compute unit averaging weights.

        This method implements exponential weights.
        """
        # Extract theta_hat of target unit
        target_params = self.ind_estimates[self._target_coord]
        # Compute weights based on exponentiated 2-norm
        raw_diff = exp(-norm(self.ind_estimates - target_params, ord=2, axis=1))
        self.weights = raw_diff / sum(raw_diff)

Important

When implementing _compute_weights(), use the processed attributes:

• self.ind_estimates: NumPy array of unit-specific estimates,

• self._target_coord: Index of the target unit in ind_estimates.

Avoid redefining __init__() unless you need additional parameters.

ExpDistUnitAverager in Practice

To illustrate ExpDistUnitAverager in action, we come back to the example from Getting Started. In short, the practical problem of interest is predicting the change in unemployment in Frankfurt in January 2020 using a panel of 150 German labor market districts, Frankfurt included.

Since ExpDistUnitAverager did not redefine the constructor from BaseUnitAverager, it needs the same two parameters: a focus function and and array/dict of individual estimates. We construct those using the same code as in Getting Started. For brevity, the full code is omitted, please see Getting Started regarding the data and inputs:

ind_estimates, _, forecast_frankfurt_jan_2020 = prepare_frankfurt_example()

averager = ExpDistUnitAverager(
    focus_function=forecast_frankfurt_jan_2020,
    ind_estimates=ind_estimates,
)

We can now fit our averager and examine the predicted value:

averager.fit(target_id="Frankfurt")
print(averager.estimate.round(3))

-0.057

Finally, as before, we can examine the fitted weights:

weight_df = pd.DataFrame({"aab": averager.keys, "weights": averager.weights})
# sphinx_gallery_thumbnail_number = 1
fig, ax = plot_germany(
    weight_df,
    "Weight in Averaging Combination: Exponential Weights",
    cmap="Purples",
    vmin=-0.005,
)

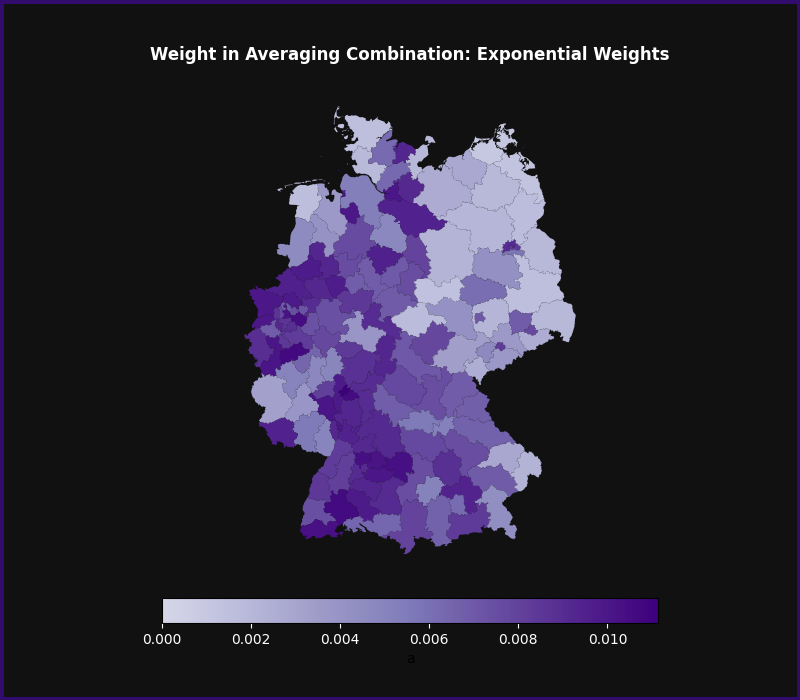
ExpDistUnitAverager spreads the weights rather broadly across Germany, with the notable exception of former East Germany. In other words, the unemployment dynamics in many regions are fairly similar to those of Frankfurt in terms of coefficients.