Introducing unit-averaging

Posted in Statistics / Machine learning on Python
Introducing unit-averaging

unit-averaging: A package for unit averaging in Python. Efficient ensemble estimation of unit-specific parameters

I’ve released version 1.0 of unit-averaging, a Python package for efficient ensemble estimation of unit-specific parameters in heterogeneous data! It’s now available on PyPI with full documentation on my web. The package automates optimal weighting, supports flexible workflows, and integrates easily into existing pipelines. In this post, I briefly outline the problem it addresses, the approach, and how to use the package.

The Problem: Estimating Individual Parameters

Let’s start with a motivating example. Imagine you want to forecast Spain’s gross domestic product (GDP) for next year. You have panel data for Spain and other European countries. How do you construct an efficient forecast?

There are two obvious options:

  • Build your forecast using only Spanish data.
  • Pool all the data and fit a single predictive model.

Neither is ideal. The first option is less biased but has higher variance and ignores most of the data. The second option likely introduces high bias, especially if the model is nonlinear or dynamic, since different countries have different economic dynamics.

This example illustrates a general problem: estimating unit-specific parameters (e.g., GDP forecasts for Spain) from a panel of units, each with its own version of the parameter (the problem of unobserved heterogeneity).

Solution: Unit Averaging

unit-averaging offers a compromise third solution called unit averaging that Christian Brownlees and I develop in a paper of ours. Unit averaging uses an ensemble of unit-level estimators. Such an ensemble can exploit panel-wide information to optimally reduce variance while controlling bias. The approach works for both nonlinear and dynamic models.

To explain the essential idea, let \(i=1, \dots, N\) be the different units in your data (countries, customers, firms; or studies in a meta-analysis). The data is heterogeneous in the sense that each unit \(i\) has their own version of some parameter \(\theta_i\).

We are interested in the unit-specific “focus parameter” \(\mu(\theta_i)\) for some fixed unit \(i\). This parameter could be predictive (e.g., GDP forecast, churn probability) or causal/structural (e.g., individual treatment effects, multipliers). The focus function \(\mu(\cdot)\) can also depend on the data of the target unit.

The goal is to estimate \(\mu(\theta_i)\) optimally, minimizing mean squared error (MSE).

The unit averaging approach has two steps:

  1. Estimate each \(\theta_i\) with the individual (or unit-specific) estimator \(\hat{\theta}_i\). Compute \(\mu(\hat{\theta}_i)\) for all \(i\).
  2. Compute a weighted average of the individual estimators:
\[\hat{\mu}(\mathbf{w}) = \sum_{i=1}^N w_i \mu(\hat{\theta}_i),\]

where the weights \(\mathbf{w} = (w_1, \dots, w_N)\) are non-negative and sum to 1.

To understand the intuition behind \(\hat{\mu}(\mathbf{w})\), suppose that we can write the individual-specific true parameters \(\theta_i\) as a sum of two pieces: \[\theta_i = \mathbb{E}[\theta_i] + \eta_i.\]

Here

  • \(\mathbb{E}[\theta_i]\) is the average value that is common to all units (e.g. broad global economic laws).
  • \(\eta_i\) is a mean-zero value that is specific to unit \(i\) (e.g. Spain-specific dynamics).

Unit averaging is motivated by the fact that each unit carries information about \(\mathbb{E}[\theta_i]\). Using data on non-target units may help reduce the uncertainty about \(\mathbb{E}[\theta_i]\) and reduce the overall variance of the estimator. By averaging \(\mu(\hat{\theta}_i)\) after estimation (not pooling data beforehand), unit averaging can exploit shared information across units without assuming a specific model form.

The Package

unit-averaging is a lightweight Python I wrote to implement unit averaging. It implement all the schemes \(\hat{\mu}(\mathbf{w})\) that we propose, including the MSE-optimal weights. I tried to design it with a few goals in mind:

  • Flexibility: the package works with panel data, meta-analysis, and other heterogeneous datasets.
  • Versatility: the implemented averagers are compatible with standard estimation packages for constructing \(\hat{\theta}_i\); minimal code changes required.
  • Speed: optimal weights are near-instant to compute even with tens of thousands of units thanks to using cvxpy in the background.
  • Customization: if the built-in schemes don’t fit your needs, you can implement your own weighting logic by subclassing the base classes.

I also tried to keep the interface simple and uniform. One should need just three line to integrate any unit averager into a pipeline that already runs individual estimators \(\hat{\theta}_i\): importing the averager class, instantiating it, and fitting the instance. For example, if you already have the individual-specific estimates (along with their matrices of covariances), you can run optimal unit averaging as

from unit_averaging import OptimalUnitAverager

averager = OptimalUnitAverager(
    focus_function=parameter_of_interest,      # focus function
    ind_estimates=estimates,                   # individual estimates
    ind_covar_ests=covariances                 # individual covariances
)

averager.fit(target_id="unit_of_interest")

After fitting, the computed \(\hat{\mu}(\mathbf{w})\) is available in the estimate attribute, ready for downstream use in place of the original unit-specific estimate.

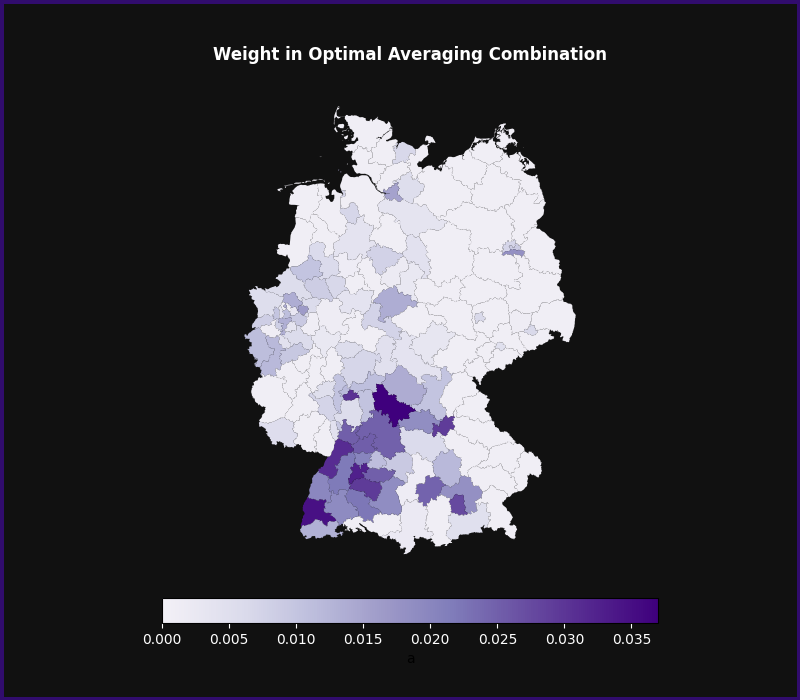
Finally, the averager also stores the fitted weights in the weights attributes. Those weights can be interesting in themselves, as they can sometimes reveal patterns in the data that are driven by similarities in the focus parameters between units. For example, when predicting unemployment in Frankfurt using data from other German regions, optimal unit averaging assigns higher weights to nearby regions and other major cities like Munich and Hamburg (see this tutorial for details).

Frankfurt map

Next Steps

Check out:

© 2025. All rights reserved.