Regression II: Model Training and Validation

Bias-variance trade-off, training models, cross-validation

Vladislav Morozov

Introduction

Lecture Info

Learning Outcomes

This lecture — second part of our illustrated regression example


By the end, you should be able to

  • Discuss bias-variance trade-off
  • Explain how to use cross-validation for model validation (generalization performance, model comparison, tuning parameter choice)
  • Use regressor predictors in scikit-learn

References


Empirical Setup

Reminder: Empirical Problem

Overall empirical goal: (R)MSE-optimal prediction of median house prices in California on the level of reasonably small blocks

Last time

  • Load the data
  • Some EDA
  • Preparation

Imports

import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
import plotly.express as px

from scipy.stats import randint, uniform

# Deeply copying objects
from sklearn.base import clone

# For composing transformations
from sklearn.compose import ColumnTransformer
from sklearn.pipeline import Pipeline

# Data source
from sklearn.datasets import fetch_california_housing

# Regression random forest
from sklearn.ensemble import RandomForestRegressor

# Linear models 
from sklearn.linear_model import (
  Lasso,
  LinearRegression,
)

# Evaluating predictor quality
from sklearn.metrics import root_mean_squared_error

# For splitting dataset
from sklearn.model_selection import (
  cross_val_score,
  GridSearchCV,
  RandomizedSearchCV,
  train_test_split
)

# For preprocessing data
from sklearn.preprocessing import(
  FunctionTransformer, 
  PolynomialFeatures,
  StandardScaler
)
 
# Regression trees
from sklearn.tree import DecisionTreeRegressor

Reminder on Data Preparation

Continue with empirical setup from last time:

  • California housing data set
  • Split 80%/20% into training/test data
  • Training set further split into X_train and y_train
Loading data 
# Load data
data = fetch_california_housing(data_home=data_path, as_frame=True)
data_df = data.frame.copy()    
# Split off test test             
train_set, test_set = train_test_split(data_df, test_size = 0.2, random_state= 1)
# Separate the Xs and the labels
X_train = train_set.drop("MedHouseVal", axis=1)
y_train = train_set["MedHouseVal"].copy()

Reminder: Geographical Representation of Data

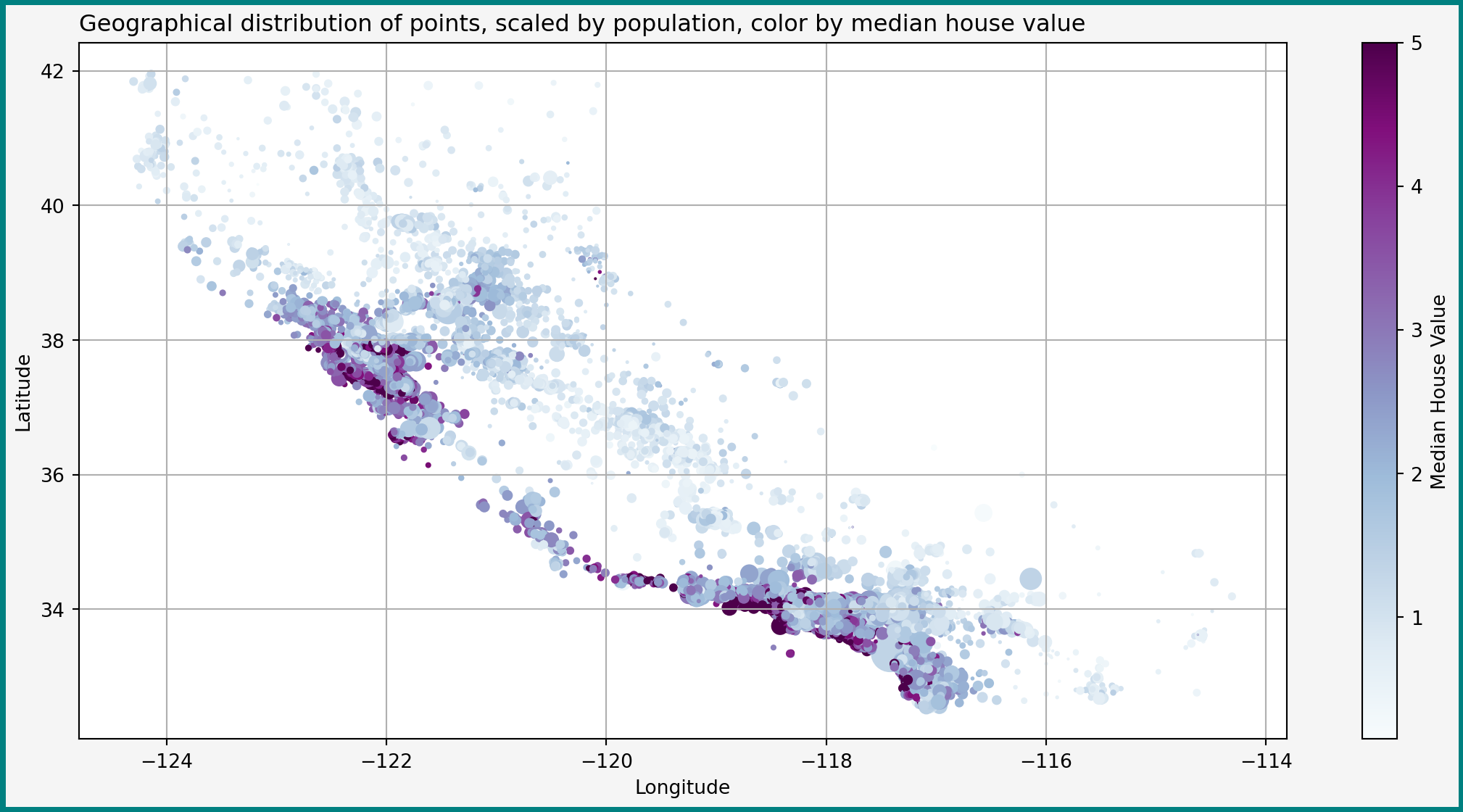
Bias-Variance Trade-Off

Current Goal: Picking \(\Hcal\)

So far have

  • Risk
  • Basic idea of the data


Now need to pick hypothesis class \(\Hcal\)

  • Guided by bias-complexity trade-off
  • Special related decomposition for MSE — the bias-variance trade-off

Bias-Variance Decomposition: Irreducible Error

Define \(U = Y- \E[Y|\bX]\) and let \(\var(U) = \sigma^2\)


  • Then (why?) \[ \E[U|\bX] =0 \]
  • \(\sigma^2\) is sometimes called the irreducible error: the risk of the best predictor \(\E[Y|\bX]\) (Bayes risk)

Bias-Variance Decomposition: Statement

Let

  • \(S\) be some sample
  • \(\hat{h}_S\) be the hypothesis picked by some algorithm
  • \(\bX\) be a new point independent of \(S\)

Then \[ \begin{aligned} \hspace{-1cm} \E_S\left[MSE(\hat{h}_S)\right] & = \sigma^2 + \E_{\bX}\left[\var_S(\hat{h}_S(\bX))\right] \\ & \quad + \E_{\bS}\left[\E_{\bX}\left[ (\E[Y|\bX]- \hat{h}_S(\bX))^2 \right]\right] \end{aligned} \]

To show the decomposition, proceed with MSE as before. See the problem set

Bias-Variance Decomposition: Interpretation

\[ \begin{aligned} \hspace{-1cm} \E_S\left[MSE(\hat{h}_S)\right] & = \sigma^2 + \E_{\bX}\left[\var_S(\hat{h}_S(\bX))\right] \\ & \quad + \E_S\left[\E_{\bX}\left[ (\E[Y|\bX]- \hat{h}_S(\bX))^2 \right]\right] \end{aligned} \tag{1}\]

MSE is sum of

  • Irreducible error \(\sigma^2\)
  • Variance of \(\hat{h}_S(\bX)\)
  • Squared bias of \(\hat{h}_S(\bX)\) for Bayes predictor \(\E[Y|\bX]\)

Bias-Variance Decomposition: Discussion

  • Note: two layers of expectations
    • With respect to sample \(S\): randomness in \(\hat{h}_S\) due to sampling
    • With respect to \(\bX\): the new independent point (definition of risk)

Have already seen such expression: exactly the kind of construction in PAC-learning — properties of risk of \(\hat{h}_S\), integrated over sample \(S\)

Bias-Variance Trade-Off

Bias-variance trade-off:

  • More complicated \(h(\bx)\) can approximate \(\E[Y|\bX=\bx]\) better
  • But complicated \(h(\cdot)\) likely has higher \(\var_S(h(\bx))\): equal changes in \(S\) may lead to larger changes in \(\hat{h}_S(\bx)\)

Bias-complexity trade-off also sometime called bias-variance trade-off by synecdoche. But, strictly speaking, only MSE can be written as \((Bias)^2 + Variance\). Other risks — different components (e.g. MAE involves absolute value of bias and mean absolute deviation)

Linear Regression

Polynomial Hypotheses

Polynomial Hypotheses

Start with familiar linear hypothesis class \[ \Hcal = \curl{h(\bx): \varphi(\bx)'\bbeta: \bbeta\in \R^{\dim(\varphi(\bb))} } \] where

  • \(\bbeta\) coefficients
  • \(\bx\) — original features
  • \(\varphi(\bx)\) — polynomials of some of the original \(\bx\) up to given degree \(k\)

Implementation Approach


Simple to do conveniently and reproducibly with scikit-learn

  1. Create Pipeline that take \(\bx\) and returns \(\varphi(\bx)\) (did that last time)
  2. Attach a learning algorithm that takes \(\varphi(\bx)\) and returns \(\hat{y}\) to the end of the pipeline

Reminder: Preprocessing Pipeline I

Recall what we did:

  • Dropped geography
  • Create new bedroom share feature
  • Created polynomials, including interactions
  • Standardized the variables


Creating the pipeline 
# Define the ratio transformers
def column_ratio(X):
    return X[:, [0]] / X[:, [1]]
def ratio_name(function_transformer, feature_names_in):
    return ["ratio"]
divider_transformer = FunctionTransformer(
  column_ratio, 
  validate=True, 
  feature_names_out = ratio_name)

# Extracting and dropping features
feat_extr_pipe = ColumnTransformer(
  [
    ('bedroom_ratio', divider_transformer, ['AveBedrms', 'AveRooms']),
    (
      'passthrough', 
      'passthrough', 
      [
        'MedInc', 
        'HouseAge', 
        'AveRooms', 
        'AveBedrms', 
        'Population', 
        'AveOccup',
      ]
    ),
    ('drop', 'drop', ['Longitude', 'Latitude'])
  ]
) 

# Creating polynomials and standardizing
preprocessing = Pipeline(
  [
    ('extraction', feat_extr_pipe),
    ('poly', PolynomialFeatures(include_bias=False)),
    ('scale', StandardScaler()),
  ]
)

Reminder: Preprocessing Pipeline II

Pipeline(steps=[('extraction',
                 ColumnTransformer(transformers=[('bedroom_ratio',
                                                  FunctionTransformer(feature_names_out=<function ratio_name at 0x0000025D8B3F6020>,
                                                                      func=<function column_ratio at 0x0000025D8B3F4EA0>,
                                                                      validate=True),
                                                  ['AveBedrms', 'AveRooms']),
                                                 ('passthrough', 'passthrough',
                                                  ['MedInc', 'HouseAge',
                                                   'AveRooms', 'AveBedrms',
                                                   'Population', 'AveOccup']),
                                                 ('drop', 'drop',
                                                  ['Longitude', 'Latitude'])])),
                ('poly', PolynomialFeatures(include_bias=False)),
                ('scale', StandardScaler())])
In a Jupyter environment, please rerun this cell to show the HTML representation or trust the notebook.
On GitHub, the HTML representation is unable to render, please try loading this page with nbviewer.org.

OLS

OLS: LinearRegression

  • Simplest learning algorithm — OLS
  • Implemented as LinearRegression() in sklearn.linear_model
  • Plan
    • First talk about predictors in isolation
    • Then attach to our pipeline

Predictors in scikit-learn

scikit-learn also has very standardized interface for predictors:

  • Hyperparameters specified when creating instance
  • Predictors have fit() methods which takes X, y (supervised) or only X (unsupervised)
  • Unlike transformers: predictors have predict() instead of transform()
  • Some predictors other methods (decision functions, predicted probabilities, etc.)

LinearRegression In Action

scikit-learn predictors generally very easy to use!

Example with original features:

ols_mod = LinearRegression()          # Create instance
ols_mod.fit(X_train, y_train)         # Fit (run OLS)
ols_mod.predict(X_train.iloc[:5, :])  # Predict for first 5 training obs
array([2.3706987 , 2.29356618, 1.23445839, 1.43788244, 3.83655553])


Can see big difference with statsmodels: scikit-learn really designed for predictive work: makes it very easy to predict and evaluate predictions, but does not have tools for inference (in the sense of testing, etc).

Attaching LinearRegression to Pipeline

  • Want our predictors to received preprocessed data
  • Simply make an extended Pipeline by adding LinearRegression() on top of preprocessing:
ols_sq_model = Pipeline(
  [
    ("preprocessing", preprocessing),
    ("ols", LinearRegression())
  ]
)

Extended Pipeline

Pipeline(steps=[('preprocessing',
                 Pipeline(steps=[('extraction',
                                  ColumnTransformer(transformers=[('bedroom_ratio',
                                                                   FunctionTransformer(feature_names_out=<function ratio_name at 0x0000025D8B3F6020>,
                                                                                       func=<function column_ratio at 0x0000025D8B3F4EA0>,
                                                                                       validate=True),
                                                                   ['AveBedrms',
                                                                    'AveRooms']),
                                                                  ('passthrough',
                                                                   'passthrough',
                                                                   ['MedInc',
                                                                    'HouseAge',
                                                                    'AveRooms',
                                                                    'AveBedrms',
                                                                    'Population',
                                                                    'AveOccup']),
                                                                  ('drop',
                                                                   'drop',
                                                                   ['Longitude',
                                                                    'Latitude'])])),
                                 ('poly',
                                  PolynomialFeatures(include_bias=False)),
                                 ('scale', StandardScaler())])),
                ('ols', LinearRegression())])
In a Jupyter environment, please rerun this cell to show the HTML representation or trust the notebook.
On GitHub, the HTML representation is unable to render, please try loading this page with nbviewer.org.

Fitting the Model

The whole pipeline can be fitted as before

ols_sq_model.fit(X_train, y_train);


Now questions:

  • Are we happy with polynomial degree? (defaulted to 2)
  • Is this model “good”?

Evaluating Training Loss

Let’s start with evaluation

  • scikit-learn implements many metrics of model quality in sklearn.metrics
  • We want root_mean_squared_error() for RMSE

Very easy to compute training set RMSE:

root_mean_squared_error(y_train, ols_sq_model.predict(X_train))
np.float64(0.716589206401369)
  • Interpretation — around $71k error
  • This is training loss (=bad)! How to evaluate accurately?

Penalized Approaches

Beyond OLS: Penalized Least Squares

Before evaluation, let’s think if we want OLS

  • Maybe want to regularize the model
  • Still have linear hypotheses \(\curl{\varphi(\bx)'\bbeta}\), but learn \(\bbeta\) differently
  • Met some other algorithms of the form \[ \hat{\bbeta} = \argmin_{\bb} \dfrac{1}{N_{S_{Tr}}}\sum_{i=1}^{N_{S_{Tr}}} (Y_i - \varphi(\bX_i)'\bb) + \alpha \Pcal(\bb) \]

Reminder: Ridge, LASSO, ElasticNet

Popular algorithms in scikit-learn:

  • Ridge (\(L^2\)): \(\norm{\bbeta}_2^2 = \sum_{k} \beta_k^2\)
  • Lasso (\(L^1\)): \(\norm{\bbeta}_1 = \sum_{k} \abs{\beta}_k\)
  • ElasticNet: \(\norm{\beta}_1 + \kappa \norm{\beta}_2^2\). Here \(\kappa\) — relative strength of \(L^1\) and \(L^2\)

The intercept (the “bias” term) is usually not penalized — not part of the \(\bbeta\) in the above notation, but treated separately.

Reason: otherwise model depends “unnaturally” on the origin chosen for \(Y_i\)

Creating a LASSO Predictor

Very easy to create a pipeline with LASSO:

lasso_model = Pipeline(
  [
    ("preprocessing", clone(preprocessing)),
    ("lasso", Lasso())
  ]
)


  • For now using the default penalty parameter \(\alpha=1\)
  • Is that a good choice?

Note that we are cloning the preprocessing pipeline, otherwise it will be the same one as in the first model

Fitting and Training Loss of LASSO

Fitting and evaluating training loss exactly as before:

# Fit model
lasso_model.fit(X_train, y_train)
# Evaluate on training sample
root_mean_squared_error(y_train, lasso_model.predict(X_train))
np.float64(1.1559103020200665)


  • LASSO doing worse in the training sample that just OLS
  • Doesn’t say anything about generalization

(Cross-)Validation

Problem: Evaluating and Selecting Models?

Accumulated questions:

  • Are our tuning parameters (=hyperparameters) specified the best way possible?
    • Maximum degree of polynomial
    • Size of penalty \(\alpha\)
  • Does adding a penalty help?

Validation

These model selection questions answered by model validation

Simple validation approach:

  1. Split training set into training set and validation set
  2. Train all the competing models on the new training set
  3. Compute risk on validation set for each model
  4. Choose model with best performance

Dividing Multiple Times: \(k\)-Fold Cross-Validation

  1. Split training data into \(k\) folds: equal-sized nonoverlapping sets \(S_j\)
  2. For \(j=1, \dots, k\)
    • Train algorithm \(\Acal\) on \(\scriptsize S_{-j}= \curl{S_1, \dots, S_{j-1}, S_{j+1}, \dots, S_k}\)
    • Estimate risk of algorithm \(\Acal\) on \(S_j\) with \(\scriptsize \hat{R}_{S_j}(\hat{h}_{S_{-j}}^{\Acal})\)
  3. Estimate overall risk of \(\Acal\) with \[\scriptsize \hat{R}(\Acal) = \dfrac{1}{k} \sum_{j=1}^k \hat{R}_{S_j}(\hat{h}_{S_{-j}}^{\Acal}) \]

Visual Example: 5-fold CV

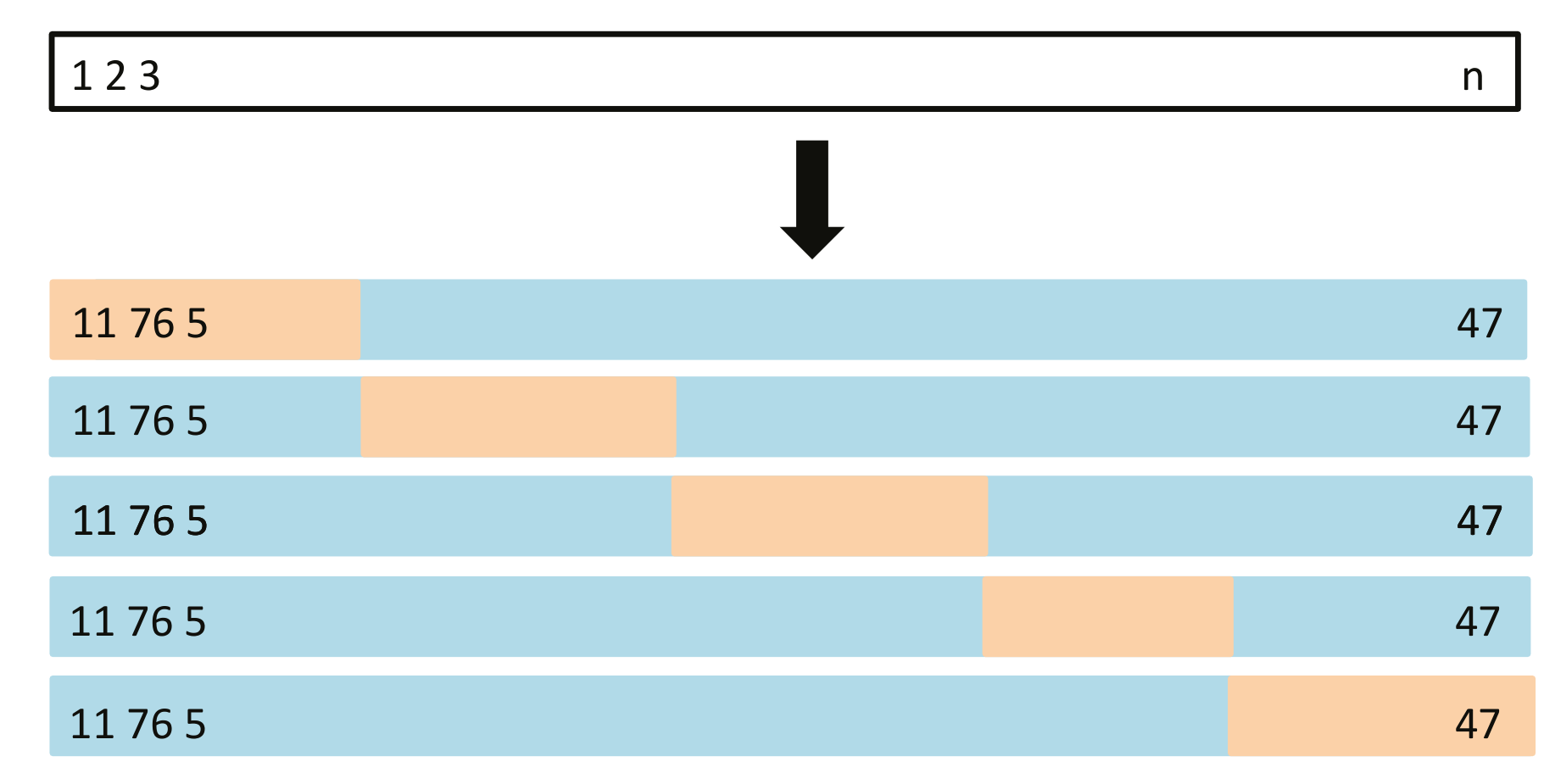
  • On step \(j\), \(j\)th fold (orange) excluded from training
  • Model trained on blue set, risk estimated on orange

Image from figure 5.5 in James et al. (2023)

Cross-Validation: Discussion

  • Here talk about algorithms (e.g. LASSO with particular \(\alpha\)):
    • \(\Acal\) might pick different \(h\) on different \(S_{-j}\)
    • Interest in risk properties of algorithms
  • Number \(k\) of folds — trade-off between computational ease and estimation quality for risk (more on that later)
  • CV — generic approach for comparing different algorithms (=choosing approaches, tuning hyperparameters)

CV in scikit-learn

scikit-learn supports CV in many forms:

  • Evaluating a specific algorithm: e.g. cross_val_score()
  • Tuning parameter choice: e.g. GridSearchCV, RandomizedSearchCV
  • Splitters for custom computations: e.g. KFold and StratifiedKFold

All in the sklearn.model_selection module

Checking Generalization Performance with CV

How good is our OLS approach with squares of features?

Use cross_val_score

ols_rmse = -cross_val_score(
    ols_sq_model,                           # algorithm
    X_train,
    y_train,
    scoring="neg_root_mean_squared_error",  # which score to compute
    cv=10,                                  # how many folds
)
  • Trains 10 times
  • Scoring: negative RMSE
  • Returns array of values: negative RMSE for each fold

Generalization Performance

pd.Series(ols_rmse).describe().iloc[:3]
count    10.000000
mean      1.616580
std       1.818678
dtype: float64
  • Recall: training loss around $71k
  • Much higher validation loss: $161k
  • But also high variance: a lot of variation between folds:
array([0.73475434, 0.73214555, 0.71531639, 6.43146961, 0.72833282,
       0.78883928, 1.45873126, 2.85839685, 0.74996918, 0.96784711])

Tuning Hyperparameters with CV

  • Can use CV to select tuning parameter \(\alpha\) and degree of polynomial
  • scikit-learn makes it easy:
    • Special classes like GridSearchCV and RandomizedSearchCV for searching parameter values
    • Just need to tell it what parameter to tune and which values to check

Tuning Penalty Parameters with CV

Example: tuning alpha in LASSO

  • Want to check 10 values between 0 and 1
  • Create a grid of values with dictionary
    • Keys: parameter name (convention: <name_in_pipeline>__<param_name>)
    • Values: an array of values to check
param_grid_alpha = { 
    "lasso__alpha": np.linspace(0, 1, 11),
}

LaasoCV and RidgeCV automatically select their penalty parameters by cross-validation — sometimes quicker

Running CV for Parameter Choice

Very similar approach to working with predictors and transformers:

  • Create instance
  • Fit
grid_search_alpha = GridSearchCV(
    lasso_model,                           # which predictor/pipeline
    param_grid_alpha,                      # parameter grids
    cv=10,                                 # number of folds
    n_jobs = -1,                           # number of parallel jobs
    scoring="neg_root_mean_squared_error", # which score
)
grid_search_alpha.fit(X_train, y_train);

Computation: estimates 10 times for each value of \(\alpha\) (110 times in total)

Viewing the Results

  • The results_ attribute has detailed info on models fitted
  • Best approach: \(\alpha\approx 0.1\). Worst: \(\alpha=0\) (OLS)
cv_res_alpha = pd.DataFrame(grid_search_alpha.cv_results_)
cv_res_alpha.sort_values(by='rank_test_score')
# Can also flip the score sign to turn into RMSE
mean_fit_time std_fit_time mean_score_time std_score_time param_lasso__alpha params split0_test_score split1_test_score split2_test_score split3_test_score split4_test_score split5_test_score split6_test_score split7_test_score split8_test_score split9_test_score mean_test_score std_test_score rank_test_score
1 0.114941 0.028044 0.009910 0.004142 0.1 {'lasso__alpha': 0.1} -0.796165 -0.761101 -0.775303 -0.800945 -0.782805 -0.780323 -0.753618 -0.785438 -0.802100 -0.778477 -0.781628 0.015090 1
2 0.114897 0.030242 0.007951 0.003047 0.2 {'lasso__alpha': 0.2} -0.816359 -0.785639 -0.805728 -0.826513 -0.805439 -0.808212 -0.773924 -0.806453 -0.826397 -0.803929 -0.805859 0.015483 2
3 0.107690 0.030768 0.006976 0.001232 0.3 {'lasso__alpha': 0.30000000000000004} -0.851757 -0.824648 -0.853041 -0.867061 -0.840383 -0.849955 -0.809561 -0.844120 -0.863233 -0.843508 -0.844727 0.016272 3
4 0.107952 0.025976 0.007243 0.001939 0.4 {'lasso__alpha': 0.4} -0.900569 -0.876197 -0.914624 -0.920610 -0.886183 -0.903635 -0.858624 -0.896340 -0.911088 -0.895341 -0.896321 0.017732 4
5 0.134578 0.029096 0.007056 0.001267 0.5 {'lasso__alpha': 0.5} -0.955774 -0.932723 -0.982019 -0.980074 -0.937986 -0.963070 -0.916799 -0.956181 -0.962360 -0.955636 -0.954262 0.019287 5
6 0.119769 0.023782 0.007964 0.002069 0.6 {'lasso__alpha': 0.6000000000000001} -1.014336 -0.992106 -1.051605 -1.043012 -0.992503 -1.025303 -0.978918 -1.017929 -1.016735 -1.020126 -1.015257 0.021449 6
7 0.135574 0.030646 0.007117 0.002224 0.7 {'lasso__alpha': 0.7000000000000001} -1.080154 -1.058064 -1.127779 -1.112880 -1.053149 -1.093986 -1.047864 -1.086479 -1.077681 -1.091080 -1.082912 0.024248 7
8 0.092308 0.003634 0.007002 0.001603 0.8 {'lasso__alpha': 0.8} -1.149506 -1.127795 -1.202201 -1.185040 -1.117950 -1.165411 -1.118929 -1.157037 -1.141068 -1.163488 -1.152843 0.026280 8
10 0.064286 0.008979 0.003399 0.000945 1.0 {'lasso__alpha': 1.0} -1.153430 -1.132308 -1.202201 -1.186119 -1.122399 -1.166705 -1.122226 -1.160035 -1.147058 -1.164363 -1.155684 0.024818 9
9 0.077912 0.009388 0.005026 0.002895 0.9 {'lasso__alpha': 0.9} -1.153430 -1.132308 -1.202201 -1.186119 -1.122399 -1.166705 -1.122226 -1.160035 -1.147058 -1.164363 -1.155684 0.024818 9
0 0.913453 0.169332 0.004534 0.003468 0.0 {'lasso__alpha': 0.0} -0.740263 -0.721958 -0.718266 -5.089013 -0.733290 -0.718058 -1.401015 -1.405668 -0.751671 -0.796095 -1.307530 1.287543 11

Tuning Multiple Parameters

  • Can tune any number of parameters we want
  • Including parameters in other parts of pipeline
  • E.g. degree of polynomial features:
param_grid = { 
    "preprocessing__poly__degree": [1, 2, 3],
    "lasso__alpha": np.linspace(0, 1, 11),
}
  • GridSearchCV called the same way
  • Computes for each combo in param_grid (330 fits total)
Calling GridSearchCV 
grid_search = GridSearchCV(
    lasso_model,
    param_grid,
    cv=10,
    n_jobs = -1,
    scoring="neg_root_mean_squared_error",
)

grid_search.fit(X_train, y_train);

Results: Tuning Linear Model

Extracting top 3 models:

param_lasso__alpha param_preprocessing__poly__degree mean_test_score std_test_score rank_test_score
0 0.0 1 -0.774210 0.016224 1
5 0.1 3 -0.779333 0.014986 2
4 0.1 2 -0.781628 0.015090 3
  • Best model: OLS with no polynomials
  • Close second and third: \(\alpha=0.1\) and polynomials of degrees 2 and 3

About Bias in Cross-Validation

Cross-validation is inherently biased

  • Final selected model — trained on full training sample of size \(N_{Tr}\)
  • But each fold fits only with \((k-1)N_{Tr}/k\) examples
    • Not the same risk performance as full sample
    • Best option: take \(k=N\) (leave-one-out CV = LOOCV) — as close as possible
  • Can’t do better if want to use all \(N_{Tr}\) examples

Model Development II: Trees and Forests

Regression Trees

Towards Trees

  • Story so far unclear whether we want nonlinearities in \(\bX\)
  • Can try a nonparametric method

New flexible hypothesis class: \[ \Hcal = \curl{\text{regression trees}} \]

Reminder: Decision Trees

  • Split the predictor space one variable at a time
  • Return same value on each rectangle \(R_k\)

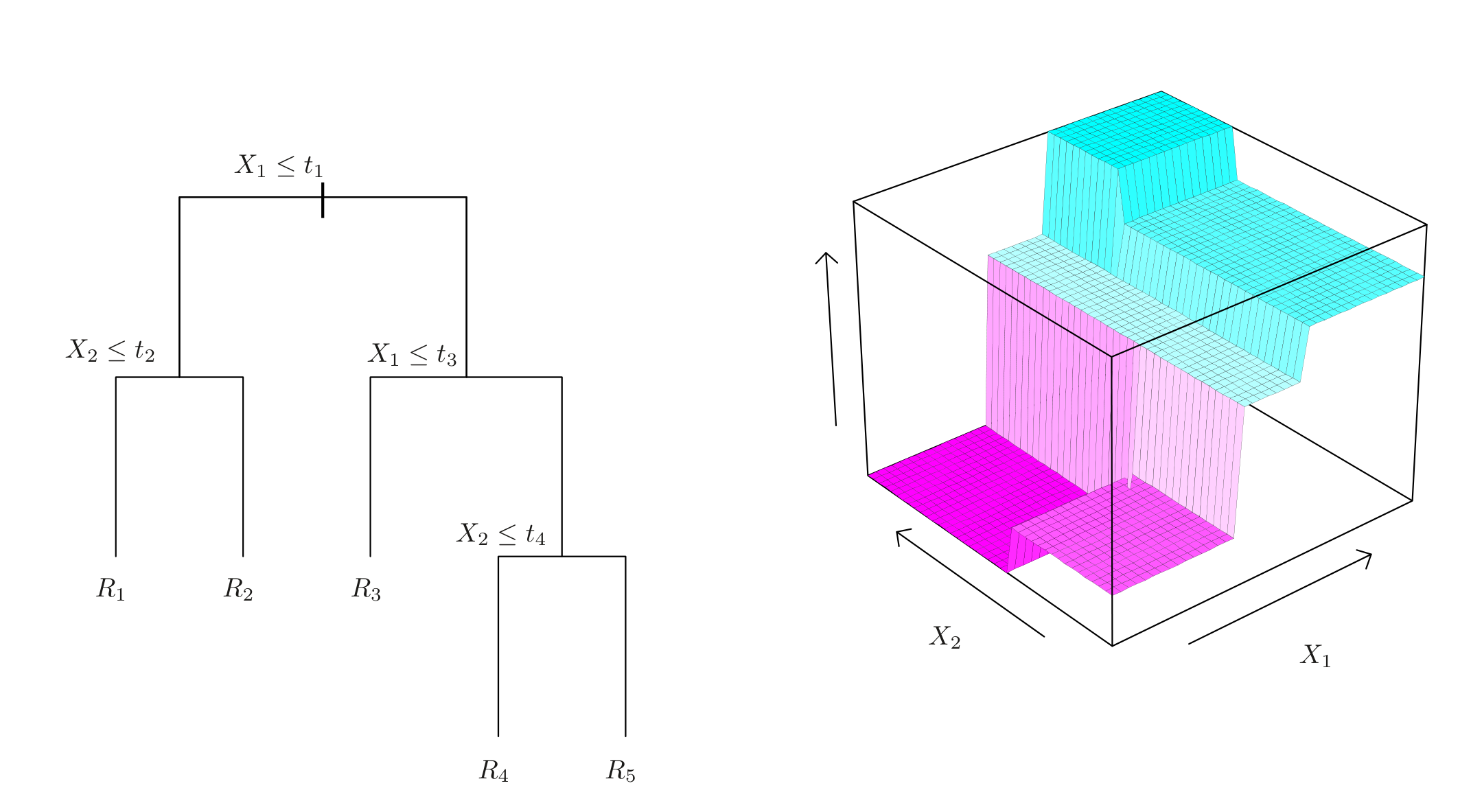
Regression trees: values can belong to \(\R\)

About Trees

Trees have a few nice features

  • Interpretable decision rules
  • No need to standardize features

Recreate preprocessing pipeline without standardization and polynomial degree = 1 (with option to tune)

Recreating preprocessing pipeline 
preprocessing = Pipeline(
  [
    ('extraction', feat_extr_pipe),
    ('poly', PolynomialFeatures(degree = 1, include_bias=False)), 
  ]
)

Trees in scikit-learn

  • scikit-learn implements trees in sklearn.tree
  • Use DecisionTreeRegressor() on top of preprocessing
tree = Pipeline(
    [
        ("preprocessing", preprocessing),
        ("tree", DecisionTreeRegressor(random_state=1)),
    ],
)

scikit-learn trains trees using the CART algorithm; see 8.1 in James et al. (2023)

Visualizing New Pipeline

Pipeline(steps=[('preprocessing',
                 Pipeline(steps=[('extraction',
                                  ColumnTransformer(transformers=[('bedroom_ratio',
                                                                   FunctionTransformer(feature_names_out=<function ratio_name at 0x0000025D8B3F6020>,
                                                                                       func=<function column_ratio at 0x0000025D8B3F4EA0>,
                                                                                       validate=True),
                                                                   ['AveBedrms',
                                                                    'AveRooms']),
                                                                  ('passthrough',
                                                                   'passthrough',
                                                                   ['MedInc',
                                                                    'HouseAge',
                                                                    'AveRooms',
                                                                    'AveBedrms',
                                                                    'Population',
                                                                    'AveOccup']),
                                                                  ('drop',
                                                                   'drop',
                                                                   ['Longitude',
                                                                    'Latitude'])])),
                                 ('poly',
                                  PolynomialFeatures(degree=1,
                                                     include_bias=False))])),
                ('tree', DecisionTreeRegressor(random_state=1))])
In a Jupyter environment, please rerun this cell to show the HTML representation or trust the notebook.
On GitHub, the HTML representation is unable to render, please try loading this page with nbviewer.org.

Training a Tree and Training Performance

Training and computing training loss exactly as before:

tree.fit(X_train, y_train)
root_mean_squared_error(y_train, tree.predict(X_train)).round(4)
np.float64(0.0)
  • We interpolated the training sample — perfect prediction
  • Generalization performance with CV:
Measuring generalization performance with CV 
tree_rmse = -cross_val_score(
    tree,
    X_train,
    y_train,
    scoring="neg_root_mean_squared_error",
    cv=10,
)
pd.Series(tree_rmse).describe().iloc[:3]
count    10.000000
mean      0.906908
std       0.025462
dtype: float64

Worse than linear methods! Overfitting problem

Why Do Tree Overfit?

  • By default, CART will grow deep trees:
    • Split space until each \(R_k\) contains only one observation
    • Each \(R_k\) predicts value of that observation \(\Rightarrow\) perfect fit
  • Trees have low bias, but very high variance
  • Changing data a bit may dramatically change tree structure

More correctly: sometimes may have examples with same \(\bX\) but different labels. Can’t split perfectly in this case

Random Forests

Ensemble Methods

An ensemble method is a predictor that combines several weaker predictors into a single (ideally) stronger one

Can combine in different ways:

  • In parallel: e.g. simple averages, as in random forest regressors
  • Sequentially: e.g. by training next predictor on errors of the previous ones, as in gradient boosting

Trees often play role of weaker predictors to be aggregated

Random Forests

A random forest is a predictor that aggregates many tree predictors


Individual trees made more distinct (decorrelated) in two ways:

  • Trained on randomized sets of data with bagging
  • Consider only a subset of variables at each split point

Bagging: Description

Consider the following approach:

  • Draw \(B\) bootstrap samples of size \(N_{Tr}\) (sample with replacement from training set)
  • On \(b\)th set train algorithm: select \(\hat{h}_{S_b}\)
  • Aggregate: in regression means averaging: \[ \hat{h}^{Bagging}(\bx) = \dfrac{1}{B} \sum_{b=1}^B \hat{h}_{S_b}(\bx) \]

In classification, may instead aggregate decisions by majority voting or by averaging predicted class probabilities

Bagging: Discussion

Bootstrap aggregation (bagging) reduces variance of a learning method by averaging many predictors trained on bootstrap samples

  • Idea: bootstrap datasets will be somewhat different from each other
  • \(\Rightarrow\) Each predictor will be a bit different
  • Averaging reduces variance

Random Forests

Random forests:

  • Do bagging
  • Make trees consider only a random subset of variables at each split
    • Idea: if you let trees use all variables, maybe will make same decisions anyway
    • Helps create even more variety

Can use RandomForestRegressor and RandomForestClassifier from sklearn.ensemble

Using RandomForestRegressor


Can attach a random forest to our pipeline

forest_reg = Pipeline(
    [
        ("preprocessing", preprocessing),
        ("random_forest", RandomForestRegressor(n_jobs=-1, random_state=1)),
    ]
)

From this can work as before

Evaluating RF with Default Tuning Parameters

Evaluating generalization performance of RF:

forest_rmse = -cross_val_score(
    forest_reg,
    X_train,
    y_train,
    scoring="neg_root_mean_squared_error",
    cv=10,
)
pd.Series(forest_rmse).describe().iloc[:3]
count    10.000000
mean      0.645291
std       0.014584
dtype: float64

This looks a lot more cheerful: validation RMSE of $64.5k — improves on linear methods

RF Tuning Parameters

Random forests have a few tuning parameters of their own. E.g:

  • How many features to consider for splitting
  • Minimum number of observations per \(R_k\)

Can also tune with cross-validation

Randomized CV useful when there are many potential parameters combinations and can’t check them all

RandomizedSearchCV

Will use randomized CV: trying random combinations of tuning parameters according to specified distribution

param_distribs = { 
    "random_forest__max_features": randint(low=2, high=5),
    "random_forest__min_samples_leaf": randint(low=1, high=50)
}

rnd_search_cv = RandomizedSearchCV( 
    forest_reg,
    param_distribs, 
    n_jobs=-1,
    n_iter=20,
    cv=10,
    scoring='neg_root_mean_squared_error',
    random_state=1,
)

Otherwise exactly same as GridSearchCV

Viewing the Results

Maybe some mild regularization with min_samples_leaf helped a bit:

CV results 
rnd_search_cv.fit(X_train, y_train)
cv_res = pd.DataFrame(rnd_search_cv.cv_results_)
cv_res.sort_values(by='rank_test_score')
mean_fit_time std_fit_time mean_score_time std_score_time param_random_forest__max_features param_random_forest__min_samples_leaf params split0_test_score split1_test_score split2_test_score split3_test_score split4_test_score split5_test_score split6_test_score split7_test_score split8_test_score split9_test_score mean_test_score std_test_score rank_test_score
16 1.708385 0.517874 1.585458 0.560056 3 8 {'random_forest__max_features': 3, 'random_for... -0.638513 -0.632746 -0.620540 -0.627392 -0.641744 -0.650287 -0.602214 -0.637370 -0.649241 -0.622942 -0.632299 0.013854 1
6 2.045547 0.405326 1.358705 0.798224 3 7 {'random_forest__max_features': 3, 'random_for... -0.640068 -0.630490 -0.621165 -0.625207 -0.642610 -0.649471 -0.603348 -0.639229 -0.650509 -0.622848 -0.632495 0.013949 2
12 2.693554 0.143107 1.512302 0.320262 4 5 {'random_forest__max_features': 4, 'random_for... -0.639521 -0.634809 -0.623402 -0.627871 -0.640666 -0.651963 -0.603616 -0.640340 -0.649286 -0.626630 -0.633810 0.013413 3
2 3.037032 0.042091 0.866206 0.464544 3 12 {'random_forest__max_features': 3, 'random_for... -0.640866 -0.631546 -0.622127 -0.630849 -0.645259 -0.654356 -0.605803 -0.638691 -0.650927 -0.625174 -0.634560 0.013869 4
5 2.233427 0.185348 0.810764 0.228408 3 13 {'random_forest__max_features': 3, 'random_for... -0.643167 -0.632400 -0.623323 -0.630358 -0.645891 -0.654325 -0.605616 -0.639778 -0.650402 -0.624979 -0.635024 0.013955 5
18 3.038652 0.237498 0.797791 0.234093 3 2 {'random_forest__max_features': 3, 'random_for... -0.643733 -0.636264 -0.626564 -0.632155 -0.642160 -0.649397 -0.606145 -0.641115 -0.652501 -0.624357 -0.635439 0.013051 6
9 2.730801 0.426022 1.001275 0.653189 4 21 {'random_forest__max_features': 4, 'random_for... -0.640357 -0.634176 -0.625298 -0.633940 -0.647881 -0.655830 -0.605672 -0.642053 -0.652009 -0.627006 -0.636422 0.014026 7
3 1.551886 0.733530 1.266785 0.512198 3 16 {'random_forest__max_features': 3, 'random_for... -0.643138 -0.635004 -0.625564 -0.633708 -0.647948 -0.654985 -0.606075 -0.641881 -0.654340 -0.628850 -0.637149 0.014049 8
7 2.804093 0.233509 0.731107 0.320225 3 21 {'random_forest__max_features': 3, 'random_for... -0.645242 -0.634204 -0.626275 -0.636459 -0.650605 -0.656446 -0.606364 -0.643166 -0.658646 -0.627800 -0.638521 0.015036 9
1 2.042244 0.818712 1.032971 0.734830 2 9 {'random_forest__max_features': 2, 'random_for... -0.647608 -0.633039 -0.625549 -0.638211 -0.651190 -0.655929 -0.607729 -0.641868 -0.657329 -0.629301 -0.638775 0.014635 10
17 2.158759 0.837695 1.473983 0.576559 3 23 {'random_forest__max_features': 3, 'random_for... -0.648433 -0.635353 -0.628195 -0.637224 -0.653057 -0.656392 -0.608144 -0.643800 -0.657045 -0.629037 -0.639668 0.014553 11
8 2.867371 0.182166 0.739058 0.357573 4 38 {'random_forest__max_features': 4, 'random_for... -0.648760 -0.640392 -0.632234 -0.642516 -0.655695 -0.662339 -0.608527 -0.647800 -0.660882 -0.635813 -0.643496 0.015072 12
13 1.673602 0.350264 1.163875 0.566846 3 31 {'random_forest__max_features': 3, 'random_for... -0.651739 -0.639499 -0.632948 -0.643117 -0.657219 -0.661390 -0.612530 -0.648216 -0.661500 -0.634261 -0.644242 0.014453 13
4 2.025969 0.371241 0.978709 0.327655 2 17 {'random_forest__max_features': 2, 'random_for... -0.650285 -0.639650 -0.635184 -0.644708 -0.658593 -0.660326 -0.614087 -0.647990 -0.662632 -0.633591 -0.644705 0.014062 14
19 2.496254 0.335675 0.295209 0.366272 2 18 {'random_forest__max_features': 2, 'random_for... -0.655762 -0.640037 -0.637039 -0.649274 -0.659356 -0.664421 -0.615996 -0.647653 -0.663497 -0.637058 -0.647009 0.014207 15
15 1.849447 0.436136 1.105208 0.280145 3 42 {'random_forest__max_features': 3, 'random_for... -0.655437 -0.642781 -0.638717 -0.649270 -0.662446 -0.665541 -0.615058 -0.650261 -0.668156 -0.637582 -0.648525 0.015130 16
0 1.074559 0.484237 1.792833 0.463905 3 44 {'random_forest__max_features': 3, 'random_for... -0.654622 -0.645104 -0.638433 -0.649766 -0.661931 -0.666774 -0.616190 -0.652332 -0.668859 -0.638484 -0.649249 0.014947 17
14 2.390857 0.117736 1.103751 0.440378 2 23 {'random_forest__max_features': 2, 'random_for... -0.660526 -0.643665 -0.640121 -0.654514 -0.662939 -0.667537 -0.618772 -0.652625 -0.670433 -0.639326 -0.651046 0.014988 18
11 2.060355 0.317073 1.164823 0.283234 2 30 {'random_forest__max_features': 2, 'random_for... -0.663953 -0.648741 -0.646561 -0.659753 -0.669645 -0.671655 -0.623958 -0.657191 -0.674384 -0.647226 -0.656307 0.014465 19
10 1.868112 0.235216 1.510497 0.443239 2 43 {'random_forest__max_features': 2, 'random_for... -0.670964 -0.656205 -0.655803 -0.669510 -0.679274 -0.678256 -0.631173 -0.666799 -0.682428 -0.651872 -0.664228 0.014883 20

Testing the Selected Model

  • Let’s select the best random forest as estimator
  • scikit-learn CV objects automatically refit the best estimator, store it in best_estimator_ attribute


Now only need to compute test error: final evaluation

X_test, y_test = test_set.drop("MedHouseVal", axis=1), test_set["MedHouseVal"].copy()
root_mean_squared_error(y_test, rnd_search_cv.best_estimator_.predict(X_test)).round(4)
np.float64(0.6302)

Recap and Conclusions

Recap


In this lecture we

  1. Discussed the bias-variance trade-off
  2. Introduced cross-validation for measuring model performance and choosing tuning parameters
  3. Saw several regressors in action with scikit-learn
    1. Polynomial regression and penalized approaches
    2. Regression trees and random forests

Next Questions


Many topics open up:

  • How does a classification problem look like? How are classification models evaluated?
  • What other learning algorithms are there? When is each one appropriate?
  • How does one deal with non-numerical features?
  • How does one deal with missing data?

References

Hastie, Trevor, Robert Tibshirani, and J. H. Friedman. 2009. The Elements of Statistical Learning: Data Mining, Inference, and Prediction. 2nd ed. Springer Series in Statistics. New York, NY: Springer.
James, Gareth, Daniela Witten, Trevor Hastie, Robert Tibshirani, and Jonathan E. Taylor. 2023. An Introduction to Statistical Learning: With Applications in Python. Springer Texts in Statistics. Cham: Springer.