Components of an ML Problem

Risk and Hypothesis Classes

Vladislav Morozov

Introduction

Lecture Info

Learning Outcomes

This lecture is about the key components of a prediction problem


By the end, you should be able to

  1. Define loss and risk functions
  2. View optimal prediction as a problem of generalization
  3. Discuss practical issues arising during risk minimization (overfitting, computational challenges, etc)

References


  • Chapter 1-2 in James et al. (2023)
  • A bit deeper: chapter 2 in Shalev-Shwartz and Ben-David (2014)

Setting

Setting

Will work only in supervised setting in this course


Setup:

  • Sample of \(N\) examples
  • All samples labeled with label \(Y_i\)
  • Features — vector of \(p\) explanatory variables \(\bX_i\)

Notice the vocabulary: ML vocabulary established and sometimes different from causal inference vocabulary

Regression and Classification

Two main kinds of supervised problems:

  1. Regression: \(Y\) continuous or close to it
  2. Classification: finite set of values for \(Y\)
    • Values of \(Y\) not necessarily ordered
    • E.g. binary classification: \(Y\) can have two values (e.g. 0 and 1)
    • Multiclass classification: \(Y\) can have more than two values (e.g. “bus”, “train”, “plane”)

Loss and Risk

Key Goal of Prediction

Key goal of prediction — predicting \(Y\) “well”

  • Other aspects: scalability, computational efficiency, interpretability
  • Difference from causal inference: there interested in causal effect of some \(X_{ij}\) on \(Y_i\)
    1. Most important: correct identification
    2. Only then efficiency/fit

How to define “well”?

Loss and Risk

Quality of prediction measured with risk function

Let \(h(\bX)\) be a prediction of \(Y\) given \(\bX\) (hypothesis)

Definition 1 Let the loss function \(l(y, \hat{y})\) satisfy \(l(y, \hat{y})\geq 0\) and \(l(y, y)=0\) for all \(y, \hat{y}\).

The risk function of the hypothesis (prediction) \(h(\cdot)\) is the expected loss: \[ R(h) = \E_{(Y, \bX)}\left[ l(Y, h(\bX)) \right] \]

Examples of Risk Functions

  • Indicator risk: \(\E[\I\curl{Y\neq h(\bX)}]\)
    • Most common in classification
    • Same price for any kind of error
  • Mean squared error \(\E[(Y - h(\bX))^2]\) and mean absolute error \(\E[\abs{Y- h(\bX)}]\)
  • Asymmetric risks such as linex: \(\E[\exp(\alpha[Y-h(\bX)]) - \alpha[Y-h(\bX)]-1]\) for \(\alpha\in \R\)
    • If \(\alpha>0\), punishes overprediction more than underprediction

Interpretation: Generalization Error

Risk measures how well the hypothesis \(h\) performs on unseen data — generalization error

Example: indicator risk: \[ \E[\I\curl{Y\neq h(\bX)}] = P(Y\neq h(\bX)) \] Probability of incorrectly predicting \(Y\) with \(h(\bX)\) — where \(Y\) and \(\bX\) are a new observation

Choosing a Risk Function

Risk function

  • Key metric of interest
  • Reflects what is directly important in your context:
    • Impact of new policy on revenue
    • Diagnosing cancer correctly
    • Flagging fraud
  • \(\Rightarrow\) choice of risk function — not a statistical question, but question of context

Risk is not necessarily the criterion function used for estimation

Empirical Risk and Hypotheses

Challenges in Choosing \(h(\cdot)\)

Ideally want to choose best possible \(h(\cdot)\): \[ \small h(\cdot) \in \argmin_{h} R(h(\cdot)) \tag{1}\] But challenges:

  1. Don’t know \(R(\cdot)\) — it depends on the true population distribution of data
  2. Can’t practically minimize over the class of all functions

Empirical Risk

Empirical Risk


Sample version of risk — empirical risk : \[ \small \hat{R}_N(h) = \dfrac{1}{N}\sum_{i=1}^N l(Y_i, h(\bX_i)). \] Average over sample \(S = \curl{(Y_1, \bX_1), \dots, (Y_N, \bX_N)}\)

Empirical Risk Minimization

Minimizing \(\hat{R}_N\) — empirical risk minimization (ERM): \[ \small \hat{h}^{ERM}_S \in \argmin_{h} \hat{R}_N(h) \]


  • ERM — theoretically among the most central learning algorithms
  • Closely tied to the actual problem of interest
  • Sometimes computationally infeasible (more on that later)

Hypothesis Classes

Issue with Minimizing Over All Functions

Minimization in Equation 1 — over all \(h\) such that the risk makes sense


Issues:

  • Computation: usually cannot search through such a large class
  • Theoretical: can overfit: fit the sample too well, generalize to unseen data poorly (more on that later)

Hypothesis Classes

Solution: look for \(h\) in some hypothesis class \(\Hcal\)

Then ERM: \[ \hat{h}_N^{ERM} \in \argmin_{h\in\Hcal} \hat{R}_N(h) \]

Careful with terminology

“Hypothesis” in ML — basically a model with specific coefficients.

Do not confuse with hypotheses in inference

Examples of Hypothesis Classes I

Popular class: linear predictors/classifiers

  • Regression: \[ \small \Hcal= \curl{h(\bx)=\varphi(\bx)'\bbeta: \bbeta\in \R^{\dim(\varphi(\bx))} } \]

  • Binary classification: \[ \small \Hcal = \curl{h(\bx) = \I\curl{\varphi(\bx)'\bbeta \geq 0}: \bbeta\in \R^{\dim(\varphi(\bx))} } \]

\(\varphi(\bx)\) — some known transformation of predictors

Example of ERM: Linear Regression I

Already know an example of ERM with specific hypothesis class — linear regression


Problem elements:

  • Risk — mean squared error
  • Hypothesis class \(\Hcal\): linear combinations of \(\bX\) of form \(h(\bx)=\bx'\bbeta\)
  • Assume \(\bX'\bX\) invertible

Example of ERM: Linear Regression II

Empirical risk minimizer: \[ \begin{aligned} \hat{h}(\bx) & = \bx'\hat{\bbeta}, \\ \hat{\bbeta} & = \argmin_{\bb} \dfrac{1}{N}\sum_{i=1}^N (Y_i - \bX_i'\bb)^2 = (\bX'\bX)^{-1}\bX'\bY \end{aligned} \]

  • Optimizing over \(\Hcal\) — same as optimizing over \(\bb\)
  • OLS — example of ERM procedure

Inductive Bias

Choice of \(\Hcal\) — part of choice of inductive bias

Definition 2 Inductive bias is the set of assumptions that the learning algorithm uses to generalize to unseen data

Examples:

  • Family of functions linking \(\bX\) and \(Y\) (e.g. linear in \(\varphi(\bX)\))
  • Or: value of \(Y\) nearly constant in small neighborhoods (as used by \(k\)-nearest neighbors regressors and classifiers)

Examples of Hypothesis Classes II: Trees I

Another approach taken by decision trees


Trees:

  • Divide predictor space into regions
  • Predict the same value for all values in a region
  • Divisions computed using recursive binary splitting

Can use both for regression and classification

Examples of Hypothesis Classes II: Trees II


  • Split the predictor space one variable at a time
  • Return same value on each rectangle \(R_k\)

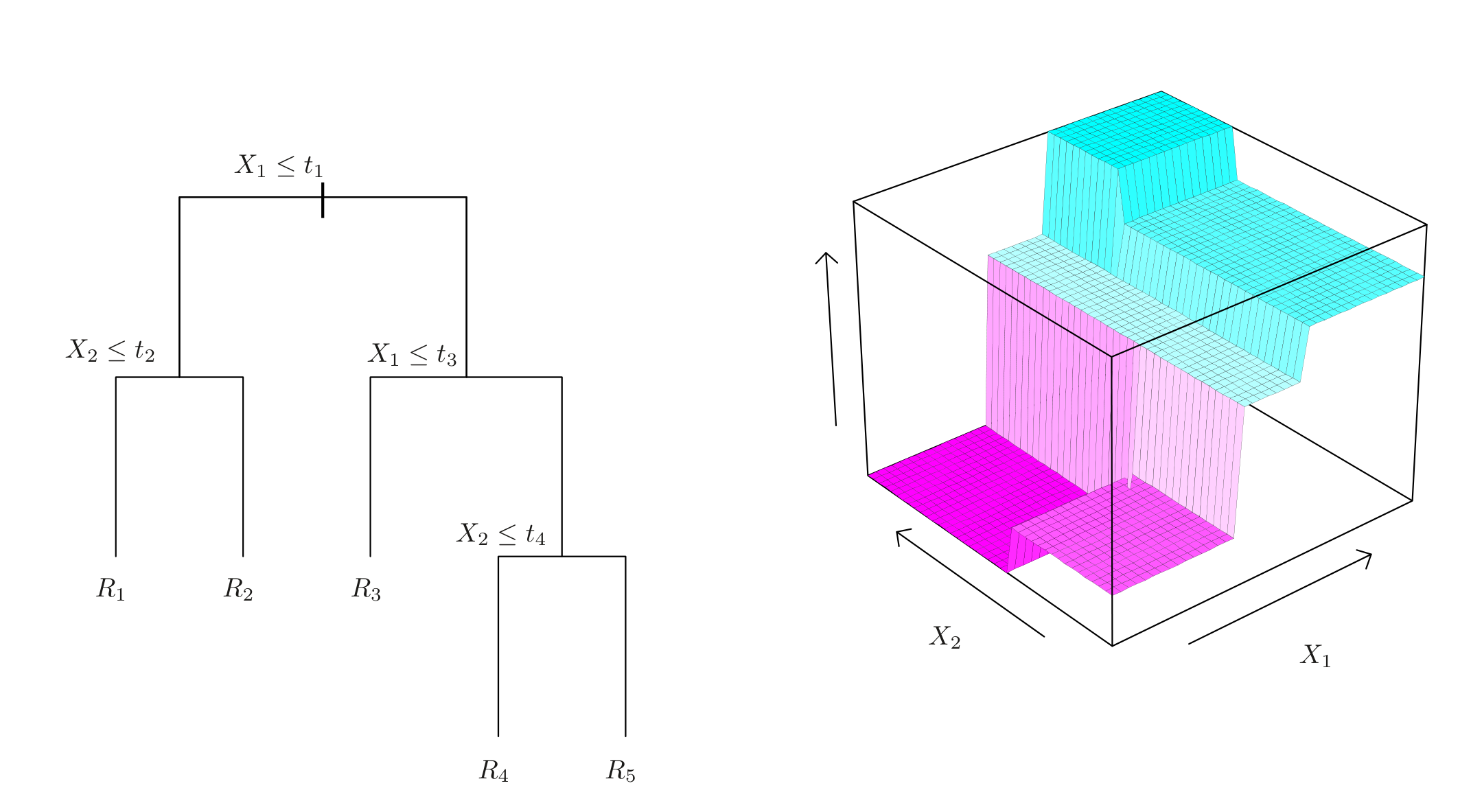
Illustration: figure 8.3 in James et al. (2023)

Beyond Simple ERM

Challenges with ERM

ERM over \(\Hcal\) \[ \small \hat{h}^{ERM}_S \in \argmin_{h \in \Hcal} \hat{R}_N(h) \]

Can still have some challenges:

  • We may want to make minimization prefer some \(h\) over others in \(\Hcal\)
  • ERM may be computationally infeasible

Penalties

Why Prefer Simpler Models?

  • Philosophically: Occam’s razor
  • Practically: overfitting
    • A more complex hypothesis can fit training data better
    • But may fit the data too closely — algorithm starts to learn noise together with data
    • Learning noise — unhelpful for generalization

Story with overfitting is more complicated thanks to “double descent”, seen especially in deep learning

Overfitting: Visual Example

Visual example — binary classification (red, blue) with two features

  • Outlined dots — unseen
  • Green — complex hypothesis, perfect on training sample
  • Black line — less complex
  • Green line generalizes worse than black (more errors on unseen points)

Image from Wikipedia

Motivational Example

Suppose: \(X\) scalar, \(\Hcal\) — polynomials up to 10th degree \[ \small \Hcal= \curl{h(x) = \sum_{k=0}^{10} \beta_k x^k, \beta\in \R^{11} } \]

  • Higher degree — more complicated explanation
  • Occam’s razor — prefer simpler explanation

How to prefer simpler explanations with ERM?

Penalties: Regularization

General answer

  • Create some positive measure of complexity \(\Pcal(h)\)
  • Add to empirical risk as a regularization (penalty) term

\[ \small \hat{h}\in\argmin_{h\in\Hcal} \hat{R}_N(h) + \lambda \Pcal(h) \tag{2}\]

\(\lambda\geq 0\) — fixed penalty parameter, controls balance between penalty and risk

Example: Ridge and Lasso

Hypothesis set: \(\Hcal= \curl{h(\bx)= \varphi(\bx)'\bbeta: \bbeta\in \R^{\dim(\varphi(\bx))}}\)

Popular penalties:

  • Ridge (\(L^2\)): \(\norm{\bbeta}_2^2 = \sum_{k} \beta_k^2\)
  • Lasso (\(L^1\)): \(\norm{\bbeta}_1 = \sum_{k} \abs{\beta}_k\)
  • Elastic net: \(\norm{\beta}_1 + \kappa \norm{\beta}_2^2\). Here \(\kappa\) — relative strength of \(L^1\) and \(L^2\)

Arise often and used in many models (see lecture on predictive regression)

Penalty Size: \(\lambda\)

\(\lambda\) in Equation 2:

  • Is a hyperparameter — parameter not chosen during training (choosing \(h\))
  • Can interpret as Lagrange multiplier for constraint \(\Pcal(h) = c\) for some \(c\)
  • Chosen during the validation step using separate data or cross-validation

Surrogate Losses

Surrogate Losses

  • ERM good: connected to minimizing actual risk
  • But sometimes ERM computationally infeasible
  • Solution: minimize some easier “surrogate” objective to find \(\hat{h}(\cdot)\)


Important

Quality of \(\hat{h}(\cdot)\) evaluated in terms of actual risk regardless

Example: Logit I

Example: binary classification (\(Y=0, 1\)) with a logit classifier based on some \(\bX\)

Classifiers indexed by \(\bbeta\): \[ \begin{aligned} h(\bx) & = \I\curl{ \Lambda( \bx'\bbeta ) \geq 0.5 }, \\ \Lambda(x) & = \dfrac{1}{1+\exp(-x)} \end{aligned} \] \(\Lambda\) — CDF of the logistic distribution

Example: Logit II


ERM to learn best \(\bbeta\) (with indicator/misclassification risk) \[ \hat{\bbeta}^{ERM} \in \argmin_{\bb} \dfrac{1}{N} \sum_{i=1}^N \I\curl{ Y_i\neq \I\curl{ \Lambda( \bX_i'\bbeta ) \geq 0.5 } } \]


Hard minimization — function is not even continuous in \(\bbeta\)

Example: Logit III

Instead of ERM can maximize the (quasi) log likelihood: \[ \small \hat{\bbeta}^{QML} = \argmax_{\bb} \sum_{i=1}^N\left[Y_i \log(\Lambda( \bX_i'\bbeta )) + (1-Y_i) \log\left( 1 - \Lambda( \bX_i'\bbeta ) \right) \right] \]

Original justification — a very specific data generating process (see 17.1 in Wooldridge (2020)).

In prediction, using maximum likelihood does not mean that you believe it — quasi means likelihood doesn’t necessarily reflect true process

Hypothesis quality checked using the actual risk — probability of predicting \(Y\) incorrectly

Example: Logit IV

  • Maximizing likelihood much easier
  • Can write \(\hat{\bbeta}^{QML}\) as \[ \small \begin{aligned} \hat{\bbeta}^{QML} & = \argmin_{\bb} \dfrac{1}{N}\sum_{i=1}^N l(Y_i, \bbeta), \\ l(Y_i, \bb) & = - \left[Y_i \log(\Lambda( \bX_i'\bbeta )) + (1-Y_i) \log\left( 1 - \Lambda( \bX_i'\bbeta ) \right) \right] \end{aligned} \] \(\hat{\bbeta}^{QML}\) — ERM under negative likelihood loss
  • Likelihood loss — “surrogate” for the target (indicator)

Example: Logit V

  • Recall: likelihood “\(\approx\)” probability of sample given \(\bbeta\)
  • \(\Rightarrow\) Another interpretation — logit classifier is learning to predict class probabilities (classes — 0, 1): \[ \widehat{P}(Y=1|\bX=x) = \Lambda(\bx'\hat{\bbeta}^{QML}) \]
  • We then compare predicted probabilities to the decision threshold 0.5

Some algorithms can return such scores or probabilities (e.g. SVMs, logit-like). Some algorithms can only return the final labels (e.g. classification trees)

Recap and Conclusions

Recap


In this lecture we

  1. Defined loss and risk
  2. Framed optimal prediction as risk minimization
  3. Introduced empirical risk minimization + penalties and surrogate losses

Next Questions


  • How do you estimate the risk of the chosen hypothesis?
  • Is there a universally valid way to predict?
  • What properties do we want our learning algorithms to have?

References

James, Gareth, Daniela Witten, Trevor Hastie, Robert Tibshirani, and Jonathan E. Taylor. 2023. An Introduction to Statistical Learning: With Applications in Python. Springer Texts in Statistics. Cham: Springer.
Shalev-Shwartz, Shai, and Shai Ben-David. 2014. Understanding Machine Learning. 1st ed. West Nyack: Cambridge University Press.
Wooldridge, Jeffrey M. 2020. Introductory Econometrics: A Modern Approach. Seventh edition. Boston, MA: Cengage.