Why Simultaneous (Joint) Tests Instead of Adjusted Multiple Tests?
Why simultaneous hypothesis tests are better — but not always — than adjusted multiple tests
When testing multiple hypotheses in a regression, why do we use simultaneous (joint) tests instead of just adjusting the \(p\)-values from separate \(t\)-tests? The usual answer is a vague statement that simultaneous tests are more powerful. This post quantifies that statement and also finds that the story is more nuanced than that.
If math is messed up, reload the page so that MathJax has another go.
Introduction
When teaching undergraduate econometrics, we eventually reach multivariate regression. This is where hypothesis testing becomes more complex — hypotheses may now involve multiple restrictions on several coefficients at the same time. To handle this, we introduce \(F\) or Wald tests, which evaluate hypotheses simultaneously (“jointly”) using a single statistic.
But is this the only way? At least in some years, the students were already familiar with the multiple testing problem and Bonferroni corrections. Naturally, the question always came up: why introduce a whole new test when we could just combine several familiar \(t\)-tests, adjusting the critical values for multiple comparisons.
My usual answer was that multiple testing adjustments ignore the structure of the problem, making them potentially less powerful. But I never had a concrete numerical example to illustrate this point.
So, I decided to take a closer look at a textbook case and run a simulation. As it turns out, the usual answer is mostly right — but not entirely. Adjusted multiple testing can indeed lead to a massive loss of power compared to simultaneous testing. However, in some cases (surprisingly!), simultaneous testing actually performs slightly worse.
Some Theory: Simultaneous vs. Multiple Testing
Specifically, to construct the example and discuss the approaches, let’s look at a simple regression model with a constant and two covariates: \[y_{i} = \alpha + \beta_1 x_i^{(1)} + \beta_2 x_i^{(2)} + u_i,\]
The null hypothesis of interest is \[H_0: \beta_1 = \beta_2 = 0.\]
This \(H_0\) is “joint” because it involves multiple parameters at once.
How do we test \(H_0\)? As I mentioned above, there are two approaches:
- Simultaneously with a single statistic.
- By combining multiple tests.
Simultaneous Tests
As soon as the above \(H_0\) is first encountered, any econometrics textbook will introduce the simultaneous testing approach. In simultaneous testing, we create a single test statistic, like the Wald statistic. The Wald test statistic \(\hat{W}\) for the above \(H_0\) is constructed using the coefficient estimates and their estimated variance-covariance matrix: \[\hat{W} = n\hat{\boldsymbol{\beta}}'(\widehat{\mathrm{Avar}}(\hat{\boldsymbol{\beta}}))^{-1}\hat{\boldsymbol{\beta}},\]
where \(n\) is the sample size, \(\hat{\boldsymbol{\beta}} = (\hat{\beta}_1, \hat{\beta}_2)\), and \(\widehat{\mathrm{Avar}}(\hat{\boldsymbol{\beta}})\) is the estimated asymptotic variance-covariance matrix of \(\hat{\boldsymbol{\beta}}\).
Under mild assumption, \(\hat{W}\) will converge in distribution to a \(\chi^2_2\) random variable. A size \(\alpha\) Wald test rejects \(H_0\) is \(\hat{W}\) exceeds the \((1-\alpha)\)th quantile of \(\chi^2_2\).
For our simple case, you can draw the decision regions of the test graphically in the space of estimates. The figure below shows the rejection region for a few different values of the correlation between \(\hat{\beta}_1\), \(\hat{\beta}_2\). If \((\hat{\beta}_1, \hat{\beta}_2)\) fall outside the yellow ellipse into the dotted area, the test rejects \(H_0\).
Multiple Tests
Combining Multiple \(t\)-Tests
Instead of testing both coefficients jointly, another approach is to test them separately and adjust for multiple comparisons. How does this work? The idea is simple: perform a \(t\)-test for each coefficient individually. If either \(t\)-test rejects, reject the joint null hypothesis.
Formally, we compute the \(t\)-statistics for the \(k\)th coefficient as \[t_k = \dfrac{\sqrt{n}\hat{\beta_k}}{\widehat{\mathrm{Avar}}(\hat{\beta}_k)}\]
A test for our \(H_0\) rejects if \(\max\lbrace |{t}_1|, |{t}_2| \rbrace\) exceeds some prespecified critical value \(c_{\alpha}\).
Critical Values and the Multiple Choice Problem
Key question: how do you set the critical value \(c_{\alpha}\) to ensure that the test has the correct size \(\alpha\)? Let’s examine the rejection probabilities under \(H_0\): \[\begin{aligned} & P(\text{test rejects}|H_0) \\ & = P(\max\lbrace |{t}_1|, |{t}_2| \rbrace \geq c_{\alpha}|H_0) \\ & = P\left( \lbrace |{t}_1| \geq c_{\alpha}\rbrace \cup \lbrace |{t}_2| \geq c_{\alpha}\rbrace |H_0 \right) \\ & = P\left( \lbrace |{t}_1| \geq c_{\alpha}\rbrace |H_0 \right) + P\left( \lbrace |{t}_2| \geq c_{\alpha}\rbrace |H_0 \right) \\ & \quad - P\left( \lbrace |{t}_1| \geq c_{\alpha}\rbrace \cap \lbrace |{t}_2| \geq c_{\alpha}\rbrace |H_0 \right), \end{aligned}\]
where we have used the inclusion-exclusion principle in the last line.
We can’t use the typical critical values from individual \(t\)-tests (i.e., the \((1-\alpha/2)\)th quantile of the \(N(0, 1)\) distribution). To see why, note that with this choice \(P\left( \lbrace |{t}_1| \geq c_{\alpha}\rbrace |H_0 \right) = \alpha\) (at least asymptotically). Meanwhile, the probability of the intersection lies somewhere between \(0\) and \(\alpha\), depending on the dependence between the test statistics. We can then conclude that \[P(\text{test rejects}|H_0) \in [\alpha, 2\alpha].\]
In words, if you do the individual \(t\)-tests with size \(\alpha\), the combination can actually have size \(2\alpha\) (e.g., 10%, if using 5% critical values). We will be rejecting the null too often even if it is true. Intuitively, there are more opportunities for large enough estimation error to slip through — see this excellent xkcd strip.
The above issue is known as the multiple testing problem. For a deeper dive into the multiple testing problem, check out chapter 9 in the excellent book by Lehmann and Romano (2022).
Bonferroni Correction
A simple solution to the problem is to simply adjust critical values in the individual component tests. If we take size-\((\alpha/2)\) critical values, the above test will reject with frequency \(\leq \alpha\) under the null — exactly what we want. That’s the idea of the Bonferroni correction, the simplest possible approach, though not the only one. In our case, if we want a test with level at most 5%, we will do the individual \(t\)-tests with values for \(2.5%\) (that is, the \(0.9875\)th quantile of the normal distribution).
So Why Simultaneous Testing?
Given that both approaches control size correctly, why do we typically prefer simultaneous tests? It’s not because they are easier to compute — simultaneous tests often require more statistical infrastructure. Instead, the key reason is power.
Recall that power, in simple terms, is the ability of a test to detect true effects. More powerful tests are more likely to reject \(H_0\) when the true parameters lie outside it — meaning they can detect real effects with higher probability.
It makes sense that simultaneous testing would be more powerful. If we look back at the rejection region image, we see that the Wald test adjusts for the dependence between \(\hat{\beta}_1\) and \(\hat{\beta}_2\), while the multiple \(t\)-test combination doesn’t. In other words, the Wald test makes better use of the available information than multiple testing adjustments.
Simulation Settings
However, intuition can be wrong and needs to be checked one way or another. To check whether it holds, let’s take a look at a simple simulation for the above model. We’ll draw \((x_{i}^{(1)}, x_{i}^{(2)})\) and \(u_{i}\) from suitable normal distributions: \[\begin{aligned} u_{i} & \sim N(0, 1), \\ \begin{pmatrix} x_i^{(1)} \\ x_i^{(2)} \end{pmatrix} & \sim N\left(\begin{pmatrix} 1 \\ 1 \end{pmatrix}, \begin{pmatrix} 1 & \rho \\ \rho & 1 \end{pmatrix} \right) \end{aligned},\]
where the correlation \(\rho\) will run between \(-1\) and \(1\). This nice normal setup reflects the canonical case first discussed in textbooks. You can also view it as an asymptotic approximation to a more general data-generating process.
To be able to visualize the results, I set \(\beta_1 = \beta_2 =c\), and then vary the common coefficient value \(c\). This setup might seem restrictive, but the results are actually quite general. By appropriately rescaling \((x_{i}^{(1)}, x_{i}^{(2)})\), any other configuration of \((\beta_1, \beta_2)\) can be reduced to a case with \(\beta_1=\beta_2\).
In this context, we can compute the power of the simultaneous Wald test and the power of adjusted multiple \(t\)-test. I’ll use the Bonferroni adjustment, and also the slightly more sophisticated Holm-Šidák method.
The full Python code for the simulations can be found in the blog GitHub repo.
Results
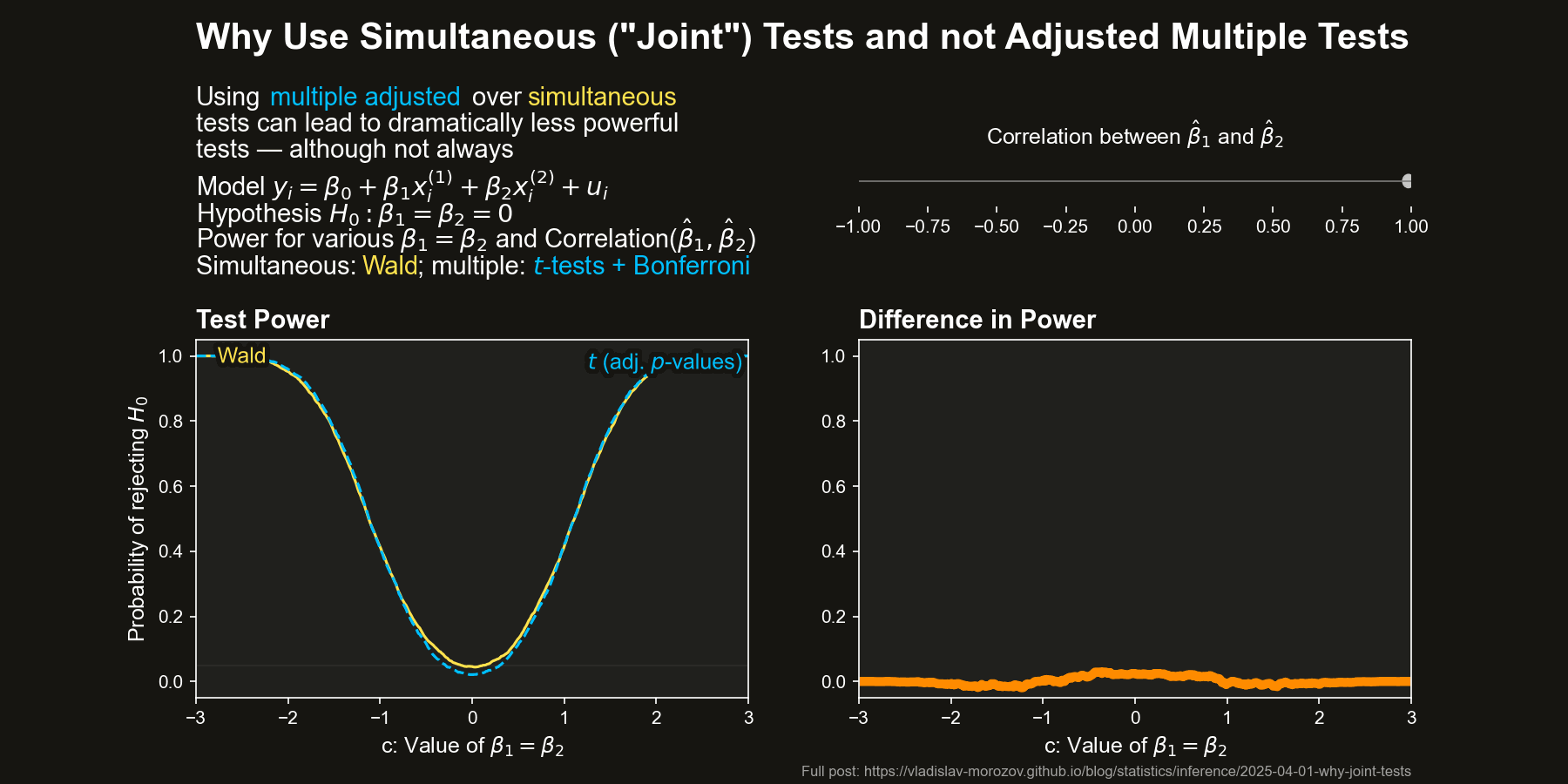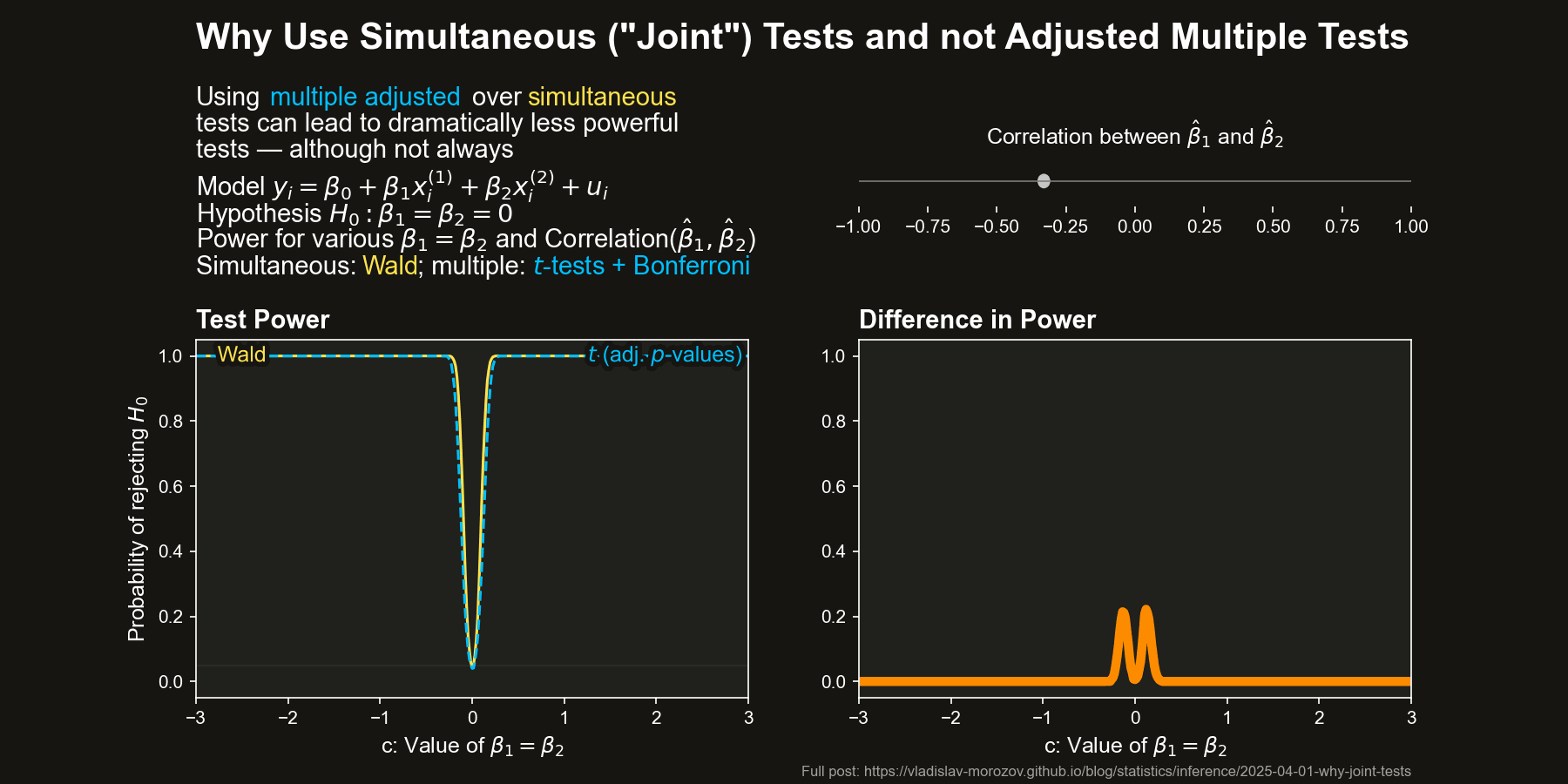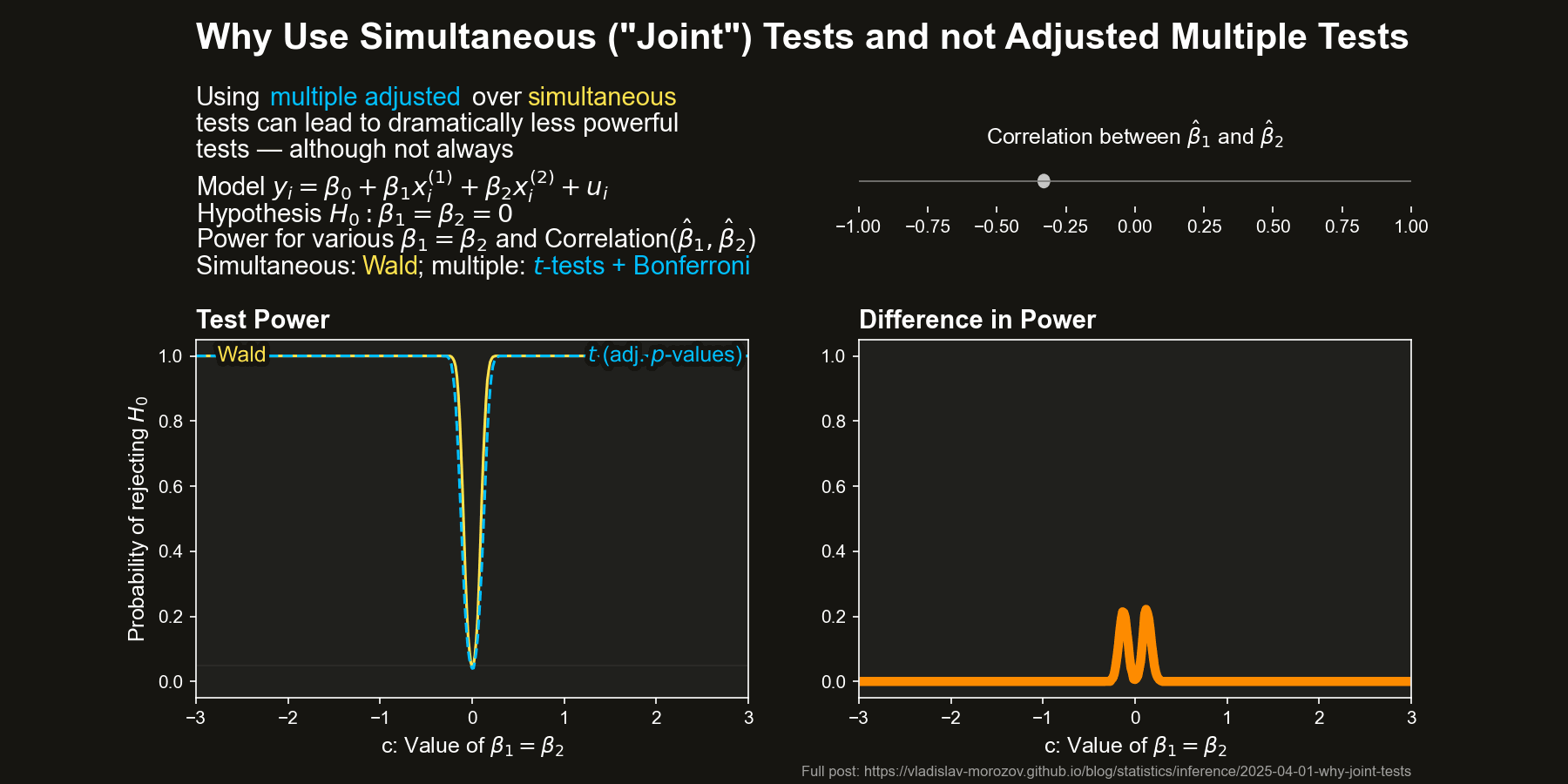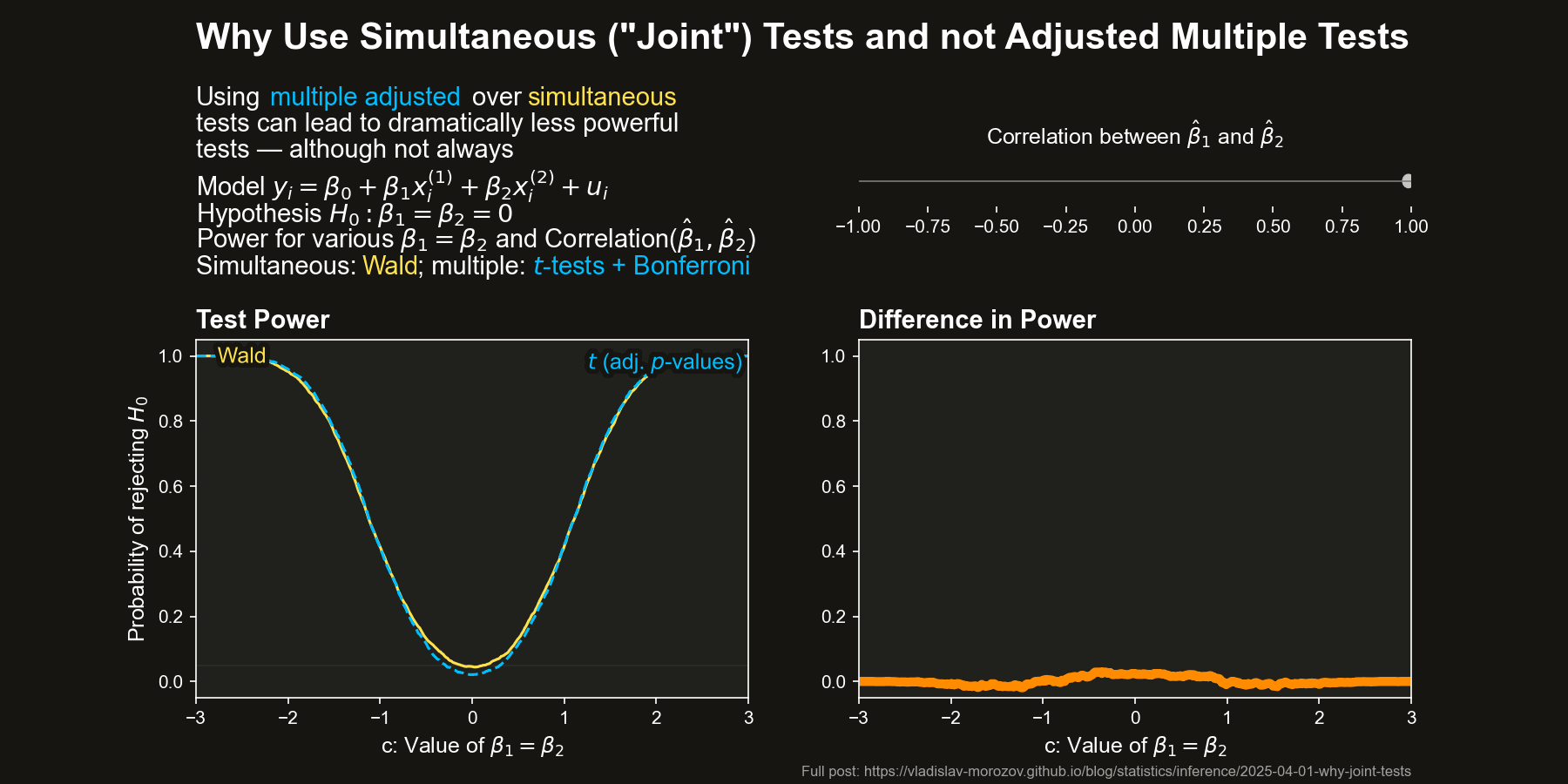
Now, let’s compare the power of simultaneous and multiple tests across different values of \(c\) and the correlation between \(\hat{\beta}_1\) and \(\hat{\beta}_2\) (approximately \(-\rho\)) The figure below depicts the difference in power between the Wald test and the two difference adjustments for the multiple \(t\)-tests, all as a function of \(c\) and the correlation between \(\hat{\beta}_1\) and \(\hat{\beta}_2\) (equal to approximately \(-\rho\)).
The differences in power are striking when the coefficient estimators are negatively correlated. In some cases, the Wald test almost always rejects \(H_0\), while the multiple \(t\)-test barely does.
To check that the above results are not due to something crazy in the test behavior, we also need to take a look at the actual power surfaces. The image below plots them on the same axes as above. See the animated plot on top of the page for a view of all the power plots for individual values of the correlation between \(\hat{\beta}_1\) and \(\hat{\beta}_2\).
Overall, it seems that both kinds of tests behave sensibly by themselves.
With the above plots in hand, I’d like to highlight three points of contrast between the tests:
Simultaneous tests can be dramatically more powerful than multiple tests when \(\hat{\beta}_1\) and \(\hat{\beta}_2\) are negatively correlated, especially for moderate deviations from \(H_0\).
This advantage fades as the correlation weakens — when \(\hat{\beta}_1\) and \(\hat{\beta}_2\) are uncorrelated, the two methods perform similarly.
For positive correlation, the Wald test actually loses some power, but the gap is much smaller than in the negative case.
In short, our intuition is only mostly right. Simultaneous tests do not always dominate multiple adjusted tests in terms of power. However, when simultaneous tests are better, they are so by such a huge margin that it is hard to imagine a situation where one would prefer the multiple testing approach.
Why the Disparity in Power?
Why does this power difference occur? And why is it more pronounced for negative correlation?
As it turns out, the case of negative and positive correlation are actually asymmetric in terms of test behavior. The image below slices out the power curves for two extreme cases:
The multiple \(t\)-test performs similarly in both cases. However, the Wald test is much better in the negatively correlated case than in the positively correlated one.
Why? This result has to do with the shape of the rejection regions and with how the coefficient estimators behave in this case. Let’s plot those regions again, this time with the line \(\beta_1=\beta_2=c\) on which the true coefficients lie:
The short story is that the power profile is determined by how much the rejection regions cover of the line \(\beta_1=\beta_2\). More of the line covered \(=\) higher power. The long story is as follows:
When \(\hat{\beta}_1\) and \(\hat{\beta}_2\) are negatively correlated, estimation errors tend to push them in opposite directions from the line \(\beta_1=\beta_2\). Under the null, these errors are likely to fall on the line \(\beta_2=-\beta_1\). The Wald test positions its rejection region accordingly and excludes a section from that line. As a result, the rejection region fails to cover only a small section of the \(\beta_1=\beta_2\) line.
In contrast, for positive correlation, estimation errors tend to move together along the \(\beta_1 = \beta_2\) line. To guarantee correct size, the Wald test has to exclude more of the line than the multiple \(t\)-tests from the rejection regions.
Finally, I want to again point out that the results are somewhat more general than they look. By suitably rescaling the covariates, one can always rescale the coefficients so that they are equal. Then the above discussion would apply in full.
Conclusion
In conclusion, the usual vague explanation that simultaneous tests are more powerful turns out to be mostly — but not always — true. While simultaneous testing does not uniformly outperform multiple testing, when it does, the improvement is substantial. Given this, it’s hard to justify using multiple testing adjustments over simultaneous tests in most practical situations. I think explaining this point with hard evidence may help people understand why we introduce and do simultaneous tests.





